В модуле Дисперсионный анализ реализованы методы общего одномерного и многомерного дисперсионного и ковариационного анализа; 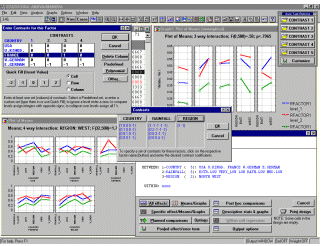 здесь можно обрабатывать планы практически неограниченной сложности. Имеется возможность задавать планы непосредственно, определив реальные переменные и уровни факторов, поэтому даже не очень опытные пользователи системы STATISTICA могут анализировать в этом модуле чрезвычайно сложные планы. По умолчанию в процедурах модуля используется подход к дисперсионному анализу, основанный на модели средних, но пользователь может также вычислить суммы квадратов типа I (последовательные, в порядке по умолчанию или заданном пользователем), типа II или типа III; для неполных планов могут также быть исследованы гипотезы типа IV. Могут быть проанализированы межгрупповые планы и планы с повторными измерениями, включая планы с расщепленными делянками, фиксированными и случайными факторами, несбалансированные и гнездовые планы и планы с изолированной контрольной группой (см. также модуль Компоненты дисперсии и смешанная модель ANOVA/ANCOVA). Для планов любого типа могут использоваться фиксированные или переменные ковариаты. Можно анализировать неполные планы (вложенные, на латинских квадратах, на греко-латинских квадратах, планы с единственным наблюдением на ячейку, рандомизированные блочные планы и т.д.); пользователь может задать объединенные члены ошибки дисперсионного анализа. Могут быть построены апостериорные критерии для маргинальных средних или для эффектов взаимодействия (включая межгрупповые факторы, факторы повторных измерений, или и те и другие): критерий наименьшей значимой разности (НЗР), критерий Ньюмена-Кеулса, критерий множественных сравнений Дункана, критерий Шеффе, критерий Тьюки достоверно значимой разности (ДЗР), обобщенный Спьотволлом и Столайном критерий Тьюки для выборок неравного размера.

Для всех основных эффектов, взаимодействий и спланированных сравнений могут быть выведены полные статистики дисперсионного анализа; программа вычисляет также множественные таблицы классификации и SSCP-матрицы. 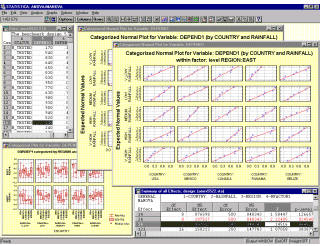 Для всех эффектов могут быть выведены таблицы результатов, в которых отмечены цветом все эффекты, уровень значимости которых выше заданного; в такой таблице, можно исследовать маргинальные средние или просмотреть мгновенные графики отдельных главных эффектов и взаимодействий, для чего достаточно просто дважды щелкнуть по эффекту. Для любых одно- и многомерных планов может быть проведен анализ контрастов неограниченной сложности. Пользователь может задавать частные эффекты взаимодействия, простые эффекты, полиномиальные контрасты и экспериментировать с произвольными комбинациями коэффициентов контраста. Имеются средства, упрощающие и ускоpяющие задание параметров в сложных анализах: в дополнение к функции Быстрое заполнение, позволяющей автоматизировать ввод коэффициентов контраста, имеется широкий выбор предопределенных контрастов, доступных по одному щелчку мыши (включая полиномиальные, отклонение, разность, Хельмерта, простые и повторные). При анализе неполных планов со случайно распределенными пропущенными ячейками процедура анализа контрастов автоматически отмечает все пустые ячейки и помогает пользователю строить проверяемые гипотезы. Большую помощь при анализе оказывают богатые графические возможности модуля (автоматическое построение графиков взаимодействий, в том числе заданных пользователем каскадов графиков компонент ("срезов") для многофакторных взаимодействий, внутригрупповых распределений переменных и внутригрупповых корреляций, определенные пользователем диаграммы размаха для медиан, квартилей, средних, стандартных отклонений, стандартных ошибок и т.д. для произвольных сочетаний факторов и многие другие, см. далее). Могут быть исследованы гипотезы параллельности (т.е. отсутствия взаимодействий, включающих ковариаты); могут быть подсчитаны полные результаты одномерной и многомерной регрессии и выведены или нарисованы скорректированные средние. Программа вычисляет также поправки Гринхауса-Гейсера и Хюнха-Фельдта для факторов повторных измерений; для таких факторов автоматически вычисляются одно- и многомерные результаты. Пользователь может исследовать SS-матрицы (сумм квадратов) гипотез и ошибок, и там, где это возможно, программа выполняет полный канонический анализ с вычислением канонических корней, собственных значений, долю дисперсии, приходящуюся на каждый корень, а также стандартизованную и нестандартизованную дискриминантную функцию (при этом нужно иметь в виду, что в модуле Дискриминантный анализ   реализована процедура полного пошагового дискриминантного анализа с расширенной диагностикой).

Для визуализации результатов при исследовании гипотез и предположений в моделях дисперсионного анализа имеется большое число различных типов графиков: графики распределений, графики ''ствол и листья", 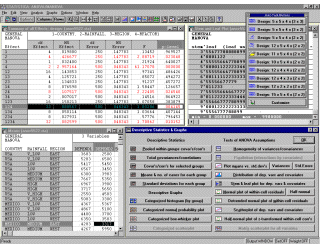 категоризованные и составные графики корреляций и подгоночных функций, позволяющие сравнивать соотношения между зависимыми измерениями (и/или) ковариатами по ячейкам высших порядков, графики средних против стандартных отклонений или дисперсий, обычные и категоризованные нормальные, полунормальные вероятностные графики и графики с исключенным трендом, графики корреляций внутри ячеек и т.д. Там, где это может потребоваться, можно одним щелчком мыши получать каскады графиков, которые затем можно просматривать в режиме, подобном демонстрации слайдов, просто нажимая кнопку Далее. Кроме того, имеется большой набор статистических процедур для проверки предположений: C Кохрена, критерий Хартли, критерий Бартлета, критерий Левена, M Бокса, непараметрический критерий Сена и Пури, критерий Колмогорова-Смирнова, критерий сферичности Моучли и т.д. При этом подгонку моделей структурированных средних (с константами), построенных по матрицам моментов для одной и нескольких выборок, можно осуществлять также средствами модуля SEPATH (Моделирование структурными уравнениями и анализ связей) системы STATISTICA, в котором можно оценивать модели MANOVA с явной неоднородностью дисперсий/ковариаций в разных группах и/или с явными структурными моделями для зависимой переменной, различными для каждой группы.