С помощью функции Подгонка распределения можно сравнить имеющееся распределение переменной с различными теоретическими распределениями. 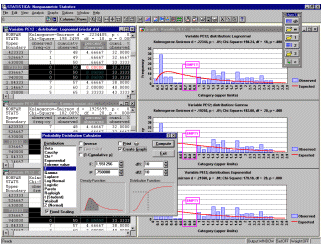 К данным можно попытаться подогнать нормальное, прямоугольное, экспоненциальное, гамма, логнормальное, хи-квадрат распределение, распределения Вейбулла, Гомпертца, биномиальное, Пуассона, геометрическое и Бернулли. Точность подгонки может быть оценена с помощью критерия хи-квадрат или одновыборочного критерия Колмогорова-Смирнова (при этом можно контролировать параметры подгонки); кроме того, реализованы также критерии Лиллиефорса и Шапиро-Уилкса (см. выше). Подгонку гипотетического распределения определенного типа к эмпирическому распределению можно осуществлять при помощи настраиваемых гистограмм (обычных и кумулятивных) с наложенными на них подгоночными функциями; прямо из таблиц результатов можно строить графики и гистограммы для ожидаемых и наблюдаемых частот, отклонений и других показателей. Ряд других методов подгонки распределения реализован в модуле Анализ процессов - здесь можно получить оценку значений параметров по принципу максимума правдоподобия для распределений: бета, экспоненциального, эстремальных значений (типа I, Гумбеля), гамма, логнормального, Релея и Вейбулла. В этом модуле имеется возможность автоматически выбрать и подогнать распределение, в наибольшей степени согласующееся с данными, а также средства подгонки распределений через моменты (с помощью кривых Джонсона и Пирсона). На диаграммы могут быть наложены (в виде кривых и поверхностей) графики заданных пользователем функций. Эти функции могут изображать самые разные типы распределений: бета, биномиальное, Коши, хи-квадрат, экспоненциальное, экстремальных значений, F, гамма, геометрическое, Лапласа, логистическое, нормальное, логнормальное, Парето, Пуассона, Рэлея, t (Стьюдента) и Вейбулла, а также их интегралы и обратные распределения. О возможностях подгонять к данным сколь угодно сложные функции предопределенных или заданных пользователем типов см. в разделе Нелинейное оценивание.