  В этом разделе перечисляются
встроенные функции Mathcad вместе с их краткими
описаниями. Эти функции подробно описаны в
главах: “Встроенные
функции” ; “Векторы
и матрицы” ; “Файлы
данных” .
Значком Е обозначены
функции, реализованные только в Mathcad PLUS.
В приведённой таблице:
- x
и y обозначают вещественные числа.
- z
обозначает число, вещественное либо
комплексное.
- m
, n, i, j и k обозначают целые
числа.
- v, u
и все имена, начинающиеся с v,
обозначают векторы.
- A
и B обозначают матрицы либо векторы.
- M
и N обозначают квадратные матрицы.
- F
обозначает векторнозначную функцию.
- file
обозначает либо имя файла, либо файловую
переменную, присоединённую к имени файла.
Все углы измеряются в радианах.
Многозначные функции и функции с комплексным
аргументом всегда возвращают главное значение.
Имена приведённых функций не чувствительны к
шрифту, но чувствительны к регистру — их следует
печатать в точности, как они приведены.
| Функция |
Возвращает... |
|
acos(z) |
арккосинус. |
|
acosh(z) |
Обращение
гиперболического косинуса |
|
angle(x, y) |
Угол между осью
абсцисс и вектором с координатами (x, y). |
|
APPEND(file) |
Добавляет число в
файл данных file. |
|
APPENDPRN(file) |
Добавляет матрицу
в структурированный файл данных file. |
|
arg(z) |
Угол в комплексной
плоскости между положительным направлением
вещественной оси и числом z. |
|
asin(z) |
Арксинус. |
|
asinh(z) |
Обращение
гиперболического синуса. |
|
atan(z) |
Арктангенс. |
|
atanh(z) |
Обращение
гиперболического тангенса. |
|
augment(A, B) |
Объединяет
матрицы-аргументы бок о бок. A и B должны
иметь одинаковый размер. |
|
|
|
|
ceil(x) |
Наименьшее целое 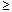 x. x
должен быть вещественным. x. x
должен быть вещественным. |
|
cfft(A) |
Быстрое
преобразование Фурье комплексных данных.
Возвращает массив того же размера, что и
аргумент. |
|
CFFT(A) |
То же, что и cfft(A),
но использует другую форму преобразования Фурье. |
|
cholesky(M) |
Нижняя
треугольная матрица L такая, что L LT = M.
Матрица M должна быть симметричной. LT = M.
Матрица M должна быть симметричной. |
|
cnorm(x) |
Функция
нормального распределения. |
|
cols(A) |
Число столбцов
массива A. Возвращает скаляр. |
|
cond1(M) |
Число
обусловленности матрицы M, основанное на
норме L1. |
|
cond2(M) |
Число
обусловленности матрицы M, основанное на
норме L2. |
|
conde(M) |
Число
обусловленности матрицы M, основанное на
евклидовой норме. |
|
condi(M) |
Число
обусловленности матрицы M, основанное на
равномерной норме. |
|
corr(A, B) |
Корреляция
массивов A и B, имеющих
одинаковый размер. |
|
cos(z) |
Косинус |
|
cosh(z) |
Гиперболический
косинус. |
|
cot(z) |
Котангенс. |
|
coth(z) |
Гиперболический
котангенс. |
|
csc(z) |
Косеканс. |
|
csch(z) |
Гиперболический
косеканс. |
|
csort(A, n) |
Сортирует столбцы
по возрастанию элементов в строке n. |
|
cspline(vx, vy) |
Коэффициенты
кубического сплайна. vx и vy вещественные
векторы одного размера. Элементы vx должны
идти в возрастающем порядке. |
|
cspline(Mxy, Mz) |
Вектор,
используемый функцией interp для интерполяции
данных из Mxy и Mz. |
|
cvar(A, B) |
Ковариация
элементов из A и B. A и B должны быть
одного размера. |
|
|
|
|
diag(v) |
Диагональная
матрица, имеющая на диагонали элементы из v. |
| Е |
dbeta(x,s1,s2) |
Плотность
бэта-распределения. |
|
dbinom(k,n,p) |
P(X = k), когда X
имеет биномиальное распределение. |
| Е |
dcauchy(x,l,s) |
Плотность
распределения Коши. |
|
dchisq(x,d) |
Плотность
хи-квадрат распределения. |
| Е |
dexp(x,r) |
Плотность
экспоненциального распределения. |
|
dF(x,d1,d2) |
Плотность
F-распределения. |
| Е |
dgamma(x,s) |
Плотность
Гамма-распределения. |
| Е |
dgeom(k, p) |
P(X = k), когда X
имеет геометрическое распределение. |
| Е |
dlnorm(x, m, s) |
Плотность
логнормального распределения. |
| Е |
dlogis(x, l, s) |
Плотность
логистического распределения. |
| Е |
dnbinom(k,n,p) |
P(X = k), когда
случайная величина X имеет отрицательное
биномиальное распределение. |
|
dnorm(x,m, s) |
Плотность
нормального распределения. |
|
dpois(k, l) |
P(X = k), когда
случайная величина X имеет распределение
Пуассона. |
|
dt(x, d) |
Плотность
распределения Стьюдента. |
|
dunif(x, a, b) |
Плотность
равномерного распределения. |
| Е |
dweibull(x, s) |
Плотность
распределения Вейбулла. |
|
|
|
|
eigenvals(M) |
Вектор из
собственных значений матрицы M. |
|
eigenvec(M, z) |
Нормированный
собственный вектор матрицы M, соответствующий
её собственному значению z. |
|
eigenvecs(M) |
Матрица, чьими
столбцами являются собственные векторы матрицы M.
Порядок расположения собственных векторов
соответствует порядку собственных значений,
возвращаемых eigenvals. |
|
exp(z) |
Экспонента ez. |
|
|
|
|
find(var1,var2, ...) |
Значения var1,var2, ..,
доставляющие решение системе уравнений. Число
возвращаемых значений равно числу аргументов. |
|
fft(v) |
Быстрое
преобразование Фурье вещественных данных. v
должен быть вещественным вектором с 2n
элементами, где n есть целое число. Возвращает
вектор размера 2n-1+1. |
|
FFT(v) |
То же, что и fft(v),
но использует другую форму преобразования Фурье.
v должен быть вещественным вектором с 2n
элементами, где n есть целое число. Возвращает
вектор размера 2n-1+1. |
|
floor(x) |
Наибольшее
целое  x.
x должен быть вещественным. x.
x должен быть вещественным. |
|
|
|
| Е |
genfit(vx,vy,vg,F) |
Возвращает вектор,
содержащий n параметров u0,u1,...un-1,
которые обеспечивают наилучшее приближение
данных из vx и vy функцией f, зависящей
от x и параметров u0,u1,...un-1. F
— функция, которая возвращает n+1-мерный
вектор, содержащий f и ее частные производные
относительно параметров. vg есть n-мерный
вектор начальных значений для n параметров. |
|
geninv(A) |
Возвращает левую
обратную к A матрицу. |
|
genvals(M, N) |
Возвращает вектор v
обобщённых собственных значений,
соответствующих решению задачи M x = vi x = vi N N x. Матрицы M и N
дожны быть вещественными. x. Матрицы M и N
дожны быть вещественными. |
|
genvecs(M, N) |
Матрица, столбцы
которой являются нормированными обобщёнными
собственными векторами. Вектор x, находящийся
в n-ом столбце является решением
задачи M x
= vn x
= vn N N x, где vn
есть соответствующий элемент вектора v, возвращаемого
genvals. x, где vn
есть соответствующий элемент вектора v, возвращаемого
genvals. |
|
|
|
|
hist(int, А) |
Возвращает вектор,
представляющий частоты, с которыми величины,
содержащиеся в векторе А, попадают в
интервалы, представляемые вектором int. |
|
|
|
|
I0(x) |
Функция Бесселя
I1. Аргумент должен быть вещественным. |
|
I1(x) |
Функция Бесселя
I2. Аргумент должен быть вещественным. |
|
In(m, x) |
Функция Бесселя
Im. x должен быть вещественным; 0 m m 100. 100. |
|
icfft(A) |
Обратное
преобразование Фурье, соответствующее cfft.
Возвращает массив того же размера, что и
аргумент. |
|
ICFFT(A) |
Обратное
преобразование Фурье, соответствующее CFFT.
Возвращает массив того же размера, что и
аргумент. |
|
identity(n) |
Единичная матрица
с числом строк n. n должно быть натуральным
числом. |
|
if(cond, x, y) |
Возвращает
значение x, если cond отличнен от 0 (истина).
Возвращает значение y, если cond равен 0
(ложь). |
|
ifft(v) |
Обратное
преобразование Фурье, соответствующее fft.
Принимает вектор размера 2n-1+1, где n -
целое. Возвращает вещественный вектор размера 2n. |
|
IFFT(v) |
Обратное
преобразование Фурье, соответствующее FFT. Принимает
вектор размера 2n-1+1, где n - целое.
Возвращает вещественный вектор размера 2n. |
|
Im(z) |
Мнимая часть z. |
|
intercept(vx, vy) |
Возвращает скаляр:
смещение по оси y линии регрессии в смысле
наименьших квадратов для данных из vx и vy. |
|
interp(vs,vx,vy,x) |
Возвращает
интерполируемое значение y, соответствующее
аргументу x. Вектор vs вычисляется на
основе векторов данных vx и vy одной из
функций lspline, pspline или cspline. |
|
interp(vs,Mxy,Mz,v) |
Возвращает
интерполируемое значение z, соответствующее
точкам x = v0 и x = v1. Вектор vs
вычисляется lspline, pspline или cspline на
основе данных из Mxy и Mz. |
|
iwave(v) |
Обратное волновое
преобразование, соответствующее wave. Берёт
вещественный вектор размера 2n, где n
есть целое число. |
|
|
|
|
J0(x) |
Функция Бесселя
J1. Аргумент должен быть вещественным. |
|
J1(x) |
Функция Бесселя
J2. Аргумент должен быть вещественным. |
|
Jn(m, x) |
Функция Бесселя
Jm. x должен быть вещественным; 0 m m 100. 100. |
|
|
|
|
K0(x) |
Функция Бесселя
K1. Аргумент должен быть вещественным. |
|
K1(x) |
Функция Бесселя
K2. Аргумент должен быть вещественным. |
|
Kn(m, x) |
Функция Бесселя
Km. x должен быть вещественным; 0 m m 100. 100. |
|
ksmooth(vx,vy,b) |
Возвращает n-мерный
вектор, созданный сглаживанием при помощи
гауссова ядра данных из vy. vy и vx есть n-мерные
векторы вещественных чисел. Параметр b управляет
окном сглаживания и должен быть установлен в
несколько раз больше величины интервала между
точками x. |
|
|
|
|
last(v) |
Индекс последнего
элемента в векторе v. |
|
length(v) |
Число элементов в
векторе v. |
|
linfit(vx, vy, F) |
Возвращает вектор,
содержащий коэффициенты, используемые, чтобы
создать линейную комбинацию функций из F,
дающую наилучшую аппроксимацию данных из
векторов vx и vy. F — функция, которая
возвращает вектор, состоящий из функций, которые
нужно oбъединить в виде линейной комбинации. |
|
linterp(vx,vy,x) |
Использует векторы
данных vx и vy, чтобы возвратить линейно
интерполируемое значение y, соответствующее
третьему аргументу x. |
|
ln(z) |
Натуральный
логарифм z. |
| Е |
loess(vx,vy,span) |
Возвращает вектор,
требуемый interp, чтобы найти набор полиномов
второго порядка, которые наилучшим образом
приближают определённые окрестности выборочных
точек, определенных в векторах vx и vy. vx
есть m-мерный вектор, содержащий координаты x.
vy есть m-мерный вектор, содержащий
координаты y, соответствующие m точкам,
определенным в vx. Аргумент span >0)
определяет, насколько большие окрестности loess
будет использовать при выполнении локального
приближения. |
| Е |
loess(Mxy,vz,span) |
Возвращает вектор,
требуемый interp, чтобы найти набор полиномов
второго порядка, которые наилучшим образом
приближают определённые окрестности выборочных
точек, определенных в массивах Mxy и vz.Mxy
есть m x 2 мерная матрица, содержащая
координаты x и у. vz есть m-мерный
вектор, содержащий координаты z,
соответствующие m точкам, определенным в Mxy.
Аргумент span >0) определяет, насколько
большие окрестности loess будет использовать
при выполнении локального приближения. |
|
log(z) |
Логарифм z по
основанию 10. |
|
lsolve(M, v) |
Вектор x такой,
что M x = v. x = v. |
|
lspline(vx, vy) |
Коэффициенты
кубического сплайна, имеющего на концах равные
нулю вторую и третью производные. vx и vy —
вещественные векторы одного размера. Элементы vx
должны идти в возрастающем порядке. |
|
lspline(Mxy, Mz) |
Вектор,
используемый функцией interp для интерполяции
данных из Mxy и Mz. Интерполирующая
поверхность имеет на границе сетки, определяемой
Mxy, равные нулю производные выше первого
порядка. |
|
lu(M) |
Матрица,
содержащая составленные бок о бок в указанном
порядке матрицы P, L и U, имеющие
одинаковый размер с M и удовлетворяющие
уравнению P M = L M = L U.
L и U есть нижняя и верхняя треугольные
матрицы соответственно. U.
L и U есть нижняя и верхняя треугольные
матрицы соответственно. |
|
|
|
|
matrix(m, n, f
) |
Cоздаёт матрицу, в
которой (i,j)-й элемент содержит f(i,j), где i
= 0, 1,...m и j = 0, 1,...n. |
|
max(A) |
Наибольший элемент
в A. Если массив A комплексный, возвращает
max(Re(A)) + i  max(Im(A)). max(Im(A)). |
|
mean(A) |
Среднее значение
элементов массива A. |
|
median(A) |
Медиана элементов
массива A. |
|
medsmooth(vy,n) |
Возвращает m-мерный
вектор, созданный сглаживанием vy с помощью
скользящей медианы. vy есть m-мерный вектор
вещественных чисел. n — ширина окна, по
которому происходит сглаживание. n должно
быть нечетным числом меньшим, чем число
элементов в vy. |
|
min(A) |
Наименьший элемент
в A. Если массив A комплексный, возвращает
min(Re(A)) + i  min(Im(A)). min(Im(A)). |
|
minerr(var1,var2, ...) |
Значения var1,var2, ... ,
доставляющие минимум функционалу невязки
системы уравнений и неравенств. Размерность
возвращаемого значения равна числу аргументов. |
|
mod(x, modulus) |
Остаток от деления x
на modulus. Аргументы должны быть вещественными.
Результат имеет тот же знак, что и x. |
|
|
|
|
norm1(M) |
L1 норма
матрицы M. |
|
norm2(M) |
L2 норма
матрицы M. |
|
norme(M) |
Евклидова норма
матрицы M. |
|
normi(M) |
Равномерная норма
матрицы M. |
|
|
|
| Е |
pbeta(x, s1, s2) |
Функция бэта-
распределения. |
|
pbinom(k, n, p) |
Функция
биноминального распределения для k
успехов в n испытаниях. |
| Е |
pcauchy(x, l, s) |
Функция
распределения Коши с параметрами масштаба l и
s. |
|
pchisq(x, d) |
Функция хи-квадрат
распределения, в которой d > 0 есть число
степеней свободы и x > 0. |
| Е |
pexp(x, r) |
Функция
экспоненциального распределения, в которой r
> 0 является параметром и x > 0. |
|
pF(x, d1, d2) |
Функция
F-распределения, в которой d1, d2 >
0 есть числа степеней свободы. x > 0. |
| Е |
pgamma(x, s) |
Функция
Гамма-распределения, в которой s > 0 есть
параметр формы. x > 0. |
| Е |
pgeom(k, p) |
Функция
геометрического распределения. p есть
вероятность успеха. k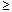 0 и 0< p 0 и 0< p  1. 1. |
| Е |
plnorm(x, m, s) |
Функция
логнормального распределения, в которой m есть логарифм среднего, s > 0 есть логарифм стандартного
отклонения и x > 0. |
| Е |
plogis(x, l, s) |
Функция
логистического распределения. l есть
параметр расположения . s > 0 есть параметр
масштаба. |
| Е |
pnbinom(k, n, p) |
Возвращает функцию
отрицательного биномиального распределения, в
котором 0< p  1. n должно быть положительным целым
числом. 1. n должно быть положительным целым
числом. |
|
pnorm(x, m, s) |
Функция
нормального распределения со средним m и среднеквадратичным отклонением s. |
|
polyroots(v) |
Корни многочлена n-ной
степени с коэффициентами, расположенными в
порядке возрастания степеней в векторе v
длины n +1. |
|
ppois(k, l) |
Функция
распределения Пуассона. l > 0. |
| Е |
predict(v, m, n) |
Возвращает n
предсказанных значений, основанных на m
последовательных значениях вектора данных v.
Элементы в v должны представлять собой
значения, взятые через равные интервалы. |
|
pspline(vx, vy) |
Коэффициенты
кубического сплайна, имеющего на концах равную
нулю третью производную. vx и vy —
вещественные векторы одного размера. Элементы vx
должны идти в возрастающем порядке. |
|
pspline(Mxy,Mz) |
Вектор,
используемый функцией interp для интерполяции
данных из Mxy и Mz. Интерполирующая
поверхность имеет на границе сетки, определяемой
Mxy, равные нулю производные третьего порядка. |
|
pt(x, d) |
Функция
распределения t-Стьюдента. d есть число
степеней свободы, x > 0 и d > 0. |
|
punif(x, a, b) |
Функция
равномерного распределения. b и a есть
концы отрезка. a < b. |
| Е |
pweibull(x, s) |
Функция
распределения Вейбулла. s > 0. |
|
|
|
| Е |
qbeta (p, s1,
s2) |
Обращает
бета-распределение с параметрами формы s1
и s2. (0  p p  1) (s1, s2 >0). 1) (s1, s2 >0). |
|
qbinom (p, n, q) |
Возвращает число
успехов в n испытаниях схемы Бернулли при
условии, что вероятность успехов не превышает p
и r — вероятность успеха на одиночном
испытании. 0 q 1 и 0 p 1. n есть
натуральное число. |
| Е |
qcauchy (p, l, s) |
Обращает
распределение Коши с параметром масштаба s и
параметром расположения l. s > 0. 0< p<1. |
|
qchisq (p, n) |
Обращает
хи-квадрат распределение, в котором d > 0
является числом степеней свободы. 0  p < 1. p < 1. |
| Е |
qexp (p, r) |
Обращает
экспоненциальное распределение, в котором r
> 0 является параметром. 0  p < 1. p < 1. |
|
qF (p, d1, d2) |
Обращает F
-распределение, в котором d1, d2
>0 являются числами степеней свободы. 0  p < 1. p < 1. |
| Е |
qgamma (p, s) |
Обращает
Гамма-распределение, в котором s > 0
является параметром формы. 0  p < 1. p < 1. |
| Е |
qgeom (p, q) |
Обращает
Гамма-распределение, в котором q > 0
является параметром формы. 0 < p < 1 и 0  q< 1. q< 1. |
| Е |
qlnorm (p, m, s) |
Обращает
логнормальное распределение, в котором m является натуральным
логарифмом среднего значения, s
> 0 - натуральный логарифм среднеквадратичного
отклонения. 0  p
< 1. p
< 1. |
| Е |
qlogis (p, l, s) |
Обращает
логистическое распределение. l — параметр
расположения, s > 0 — параметр масштаба. 0 < p
< 1. |
| Е |
qnbinom (p, n, q) |
Обращает
отрицательное биномиальное распределение с
числом испытаний n и вероятностью успеха в
одиночном испытании q. 0 < q  1 и 0 1 и 0  p p  1. 1. |
|
qnorm (p, m, s) |
Обращает
нормальное распределение со средним m и среднеквадратичным отклонением s. 0 < p < 1 и s
> 0. |
|
qpois (p, l) |
Обращает
распределение Пуассона. l > 0
и 0  p p  1. 1. |
|
qr(A) |
Матрица, чьи первые
n столбцов содержат квадратную
ортонормированную матрицу Q, а оставшиеся
столбцы содержат верхнюю треугольную матрицу R.
Матрицы Q и R удовлетворяют уравнению A
= Q R, где A
есть вещественный массив. R, где A
есть вещественный массив. |
|
qt (p, d) |
Обращает t-распределение
Стьюдента. d -число степеней свободы. d >
0 и 0 < p < 1. |
|
qunif (p, a, b) |
Обращает
равномерное распределение. b и a —
граничные точки интервала. a < b и 0  p p  1. 1. |
| Е |
qweibull (p, s) |
Обращает
распределение Вейбулла. s > 0 и 0 < p
< 1. |
|
|
|
|
rank(A) |
Ранг вещественной
матрицы A. |
| Е |
rbeta (m, s1, s2) |
Возвращает вектор m
случайных чисел, имеющих бэта-распределение. s1,
s2 > 0 есть параметры формы. |
|
rbinom (m, n, p) |
Возвращает вектор m
случайных чисел, имеющих биномиальное
распределение. 0  p p  1.
n есть натуральное число. 1.
n есть натуральное число. |
| Е |
rcauchy (m, l, s) |
Возвращает вектор m
случайных чисел, имеющих распределение Коши. s
> 0 есть параметр масштаба. l — параметр
расположения. |
|
rchisq (m, d) |
Возвращает вектор
m случайных чисел, имеющих распределение
хи-квадрат. d > 0 есть число степеней
свободы. |
|
Re(z) |
Вещественная часть
числа z. |
|
READ( file) |
Считывает
одиночное значение из файла данных file. |
|
READPRN( file) |
Считывает матрицу
из структурированного файла данных file. |
|
regress(vx, vy, n) |
Возвращает вектор,
требуемый interp, чтобы найти полином порядка n,
который наилучшим образом приближает данные из vx
и vy. vx есть m-мерный вектор, содержащий
координаты x. vy есть m-мерный вектор,
содержащий координаты y соответствующие m
точкам, определенным в vx. |
|
regress(Mxy,vz, n) |
Возвращает вектор,
требуемый interp, чтобы найти полином порядка n,
который наилучшим образом приближает данные из Mxy
и vz. Mxy есть m x 2 - мерная матрица,
содержащая координаты x-y. vz есть m-мерный
вектор, содержащий координаты z
соответствующие m точкам, определенным в Mxy. |
|
reverse(v) |
Обращает порядок
элементов вектора v. |
| Е |
rexp (m, r) |
Возвращает вектор m
случайных чисел, имеющих экспоненциальное
распределение. r > 0 — параметр
распределения. |
|
rF (m, d1, d2) |
Возвращает вектор m
случайных чисел, имеющих F -распределение. d1,
d2 > 0 есть числа степеней свободы. |
| Е |
rgamma (m, s) |
Возвращает вектор m
случайных чисел, имеющих гамма- распределение, s
> 0 есть параметр формы. |
| Е |
rgeom (m, p) |
Возвращает вектор m
случайных чисел, имеющих геометрическое
распределение. 0 < p  1. 1. |
| Е |
rlnorm (m, m, s) |
Возвращает вектор m
случайных чисел, имеющих логнормальное
распределение, в котором m я
вляется натуральным логарифмом среднего
значения, а s > 0 есть
натуральный логарифм среднеквадратичного
отклонения. |
| Е |
rlogis (m, l, s) |
Возвращает вектор
m случайных чисел, имеющих логистическое
распределение, в котором l является п а
раметром расположения, а s > 0 есть
параметр масштаба. |
| Е |
rnbinom (m, n, p) |
Возвращает вектор m
случайных чисел, имеющих отрицательное
биномиальное распределение. 0 < p  1. n есть
натуральное число. 1. n есть
натуральное число. |
|
rnd(x) |
Возвращает
равномерно распределенное случайное число между
0 и x. |
|
rnorm (m, m, s) |
Возвращает вектор m
случайных чисел, имеющих нормальное
распределение. s > 0. |
|
root(f(var), var) |
Значение var,
доставляющее нулевое значение выражению expr. |
|
rows(A) |
Число строк в
массиве A. |
|
rpois (m, l) |
Возвращает вектор m
случайных чисел, имеющих распределение Пуассона.
l > 0. |
|
rref(A) |
Ступенчатая форма
матрицы A. |
|
rsort(A, n) |
Сортирует строки в
порядке возрастания элементов из столбца n. |
|
rt (m, d) |
Возвращает вектор m
случайных чисел, имеющих t-распределение
Стьюдента. d > 0. |
|
runif (m, a, b) |
Возвращает вектор m
случайных чисел, имеющих равномерное
распределение, в котором b и a являются
граничными точками интервала. a < b. |
| Е |
rweibull (m, s) |
Возвращает вектор m
случайных чисел, имеющих распределение
Вейбулла, в котором s > 0 является
параметром формы. |
|
|
|
|
sec(z) |
Секанс. |
|
sech(z) |
Гиперболический
секанс. |
|
sin(z) |
Синус. |
|
sinh(z) |
Гиперболический
синус. |
|
slope(vx, vy) |
Возвращает скаляр:
наклон линии регрессии в смысле наименьших
квадратов для данных из vx и vy. |
|
sort(v) |
Сортирует элементы
вектора v. |
|
stack(A, B) |
Массив, созданный
помещением матрицы A над матрицей B.
Массивы A и B должны иметь одинаковое
количество столбцов. |
|
stdev(A) |
Возвращает
среднеквадратичное отклонение (квадратный
корень из дисперсии) элементов m x n массива A. |
|
submatrix(A,ir,jr,ic,jc) |
Субматрица A,
состоящая из всех элементов, находящихся на
пересечении строк с ir по jr и столбцов с ic
по jc. Чтобы сохранить порядок строк и/или
столбцов, удостоверьтесь, что ir 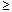 jr и ic jr и ic 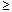 jc, иначе порядок
будет обращён. jc, иначе порядок
будет обращён. |
| Е |
supsmooth(vx,vy) |
Возвращает n-мерный
вектор, созданный локальным использованием
симметричной линейной процедуры сглаживания
методом наименьших квадратов по правилу k-ближайших
соседей, в которой k выбирается адаптивно. vy
и vx есть n-мерные векторы вещественных
чисел. Элементы vx должны быть расположены в
порядке возрастания. |
|
svd(A) |
Матрица,
составленная из расположенных друг над другом
матриц U и V, где U (расположена сверху)
есть m x n матрица и V есть n x n
матрица. Матрицы U и V удовлетворяют
равенству A = U diag(s) diag(s) VT, где s есть
вектор, который содержит n элементов,
возвращаемых функцией svds(A). A есть m x n
вещественный массив, где m VT, где s есть
вектор, который содержит n элементов,
возвращаемых функцией svds(A). A есть m x n
вещественный массив, где m 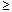 n. n. |
|
svds(A) |
Вектор, содержащий
сингулярные значения m x n вещественного
массива A, где m 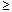 n. n. |
|
|
|
|
tan(z) |
Тангенс. |
|
tanh(z) |
Гиперболический
тангенс. |
|
tr(M) |
След квадратной
матрицы M. |
|
|
|
|
until(x, y) |
Возвращает y до
тех пор, пока x не станет отрицательным. |
|
|
|
|
var(A) |
Возвращает
дисперсию элементов массива A размерности m
x n. |
|
|
|
|
wave(v) |
Дискретное
волновое преобразование вещественных данных,
использующее четырёхкоэффициентный волновой
фильтр Даубечи. Вектор v должен содержать 2n
вещественных значений, где n есть целое число. |
|
WRITE( file) |
Записывает
одиночное значение в файл данных file. |
|
WRITEPRN( file) |
Записывает матрицу
в структурированный файл данных file. |
|
|
|
|
Y0(x) |
Функция Бесселя
Y1. Аргумент должен быть вещественным. |
|
Y1(x) |
Функция Бесселя
Y2. Аргумент должен быть вещественным. |
|
Yn(m, x) |
Функция Бесселя
Ym. x должен быть вещественным; 0 m m 100. 100. |
|
|
|
|
d(x, y) |
Символ Кронекера.
Возвращает 1, если m = n; иначе 0. Оба аргумента
должны быть целочисленными. |
|
e(i, j, k) |
Полностью
антисимметричный тензор ранга 3. i, j и k
должны быть целыми числами между 0 и 2
включительно (или между ORIGIN и ORIGIN + 2 включительно,
если ORIGIN 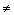 0).
Результат 0, если любые два аргумента
одинаковы, 1 для четных перестановок, -1 для
нечетных перестановок. 0).
Результат 0, если любые два аргумента
одинаковы, 1 для четных перестановок, -1 для
нечетных перестановок. |
|
G(z) |
Возвращает
значение эйлеровой гамма-функции в z. |
|
F(x) |
Cтупенчатая
функция Хэвисайда. Возвращает 1, если x 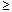 0; иначе 0. 0; иначе 0. |
  
|

