  Mathcad
включает ряд функций для вычисления регрессии.
Обычно эти функции создают кривую или
поверхность определенного типа, которая в
некотором смысле минимизирует ошибку между
собой и имеющимися данными. Функции отличаются
прежде всего типом кривой или поверхности,
которую они используют, чтобы аппроксимировать
данные.
В отличие от функций интерполяции, обсужденных
в предыдущем разделе, эти функции не требуют,
чтобы аппроксимирующая кривая или поверхность
проходила через точки данных. Функции регрессии,
рассмотренные в этом разделе, следовательно,
гораздо менее чувствительны к ошибкам данных,
чем функции интерполяции. В отличие от функций
сглаживания, рассматриваемых в следующем
разделе, конечный результат регрессии — функция,
с помощью которой можно оценить значения в
промежутках между заданными точками.
Всякий раз, когда массивы используются в любой
из функций, описанных в этом разделе, убедитесь,
что каждый элемент в массиве содержит
определённое значение, поскольку Mathcad
присваивает 0 любым элементам, которые явно не
определены.
Линейная регрессия
Эти функции возвращают наклон и смещение линии,
которая наилучшим образом приближает данные в
смысле наименьших квадратов. Если поместить
значения x в вектор vx и соответствующие
значения y в vy, то линия определяется в
виде
y = slope(vx, vy) x + intercept(vx, vy) x + intercept(vx, vy)
| slope(vx, vy) |
Возвращает скаляр: наклон линии
регрессии в смысле наименьших квадратов для
данных из vx и vy. |
| intercept(vx, vy) |
Возвращает скаляр: смещение по
оси ординат линии регрессии в смысле наименьших
квадратов для данных из vx и vy. |
Рисунок 9 показывает, как можно
использовать эти функции, чтобы провести линию
через набор выборочных точек.
Эти функции полезны не только, когда данные по
существу должны представлять линейную
зависимость, но и когда они представляют
экспоненциальную зависимость. Например, если x
и y связаны соотношением вида
y = Aekx,
можно применить эти функции к логарифму данных
и использовать тот факт, что
log(y) = log(A) + kx
В этом случае
A = exp(intercept(vx, vy)) и k = slope(vx, vy)
Такое приближение взвешивает ошибки
по-другому, нежели приближение показательной
функцией в смысле наименьших квадратов, но
обычно это — хорошая аппроксимация.
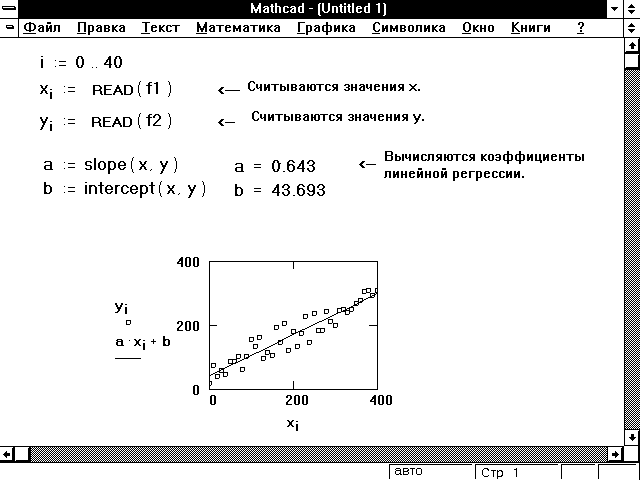
Рисунок 9: Использование функций slope и intercept для
линейной регрессии.
Полиномиальная регрессия
Эти функции полезны, когда есть набор
измеренных сответствующих значений y и x,
между которыми ожидается полиномиальная
зависимость, и нужно приблизить эти значения с
помощью полинома наилучшим в определённом
смысле образом.
Используйте regress, когда нужно использовать
единственный полином, чтобы приблизить
все данные. Функция regress допускает
использование полинома любого порядка. Однако на
практике не следует использовать степень
полинома выше n = 4.
Так как regress пытается приблизить все точки
данных, используя один полином, это не даст
хороший результат, когда данные не связаны
единой полиномиальной зависимостью. Например,
предположим, ожидается, что зависят линейно от x
в диапазоне от x1 до x10 и ведут себя
подобно кубическому полиному в диапазоне от x11
до x20. Если используется regress с n = 3,
можно получить хорошее приближение для второй
половины, но ужасное — для первой. Функция loess
облегчает эти проблемы, выполняя локальное
приближение. Вместо создания одного полинома,
как это делает regress, loess создаёт различные
полиномы второго порядка в зависимости от
расположения на кривой.
Она делает это, исследуя данные в малой
окрестности точки, представляющей интерес.
Аргумент span управляет размером этой
окрестности. По мере того как диапазон
становится большим, loess становится
эквивалентным regress с n = 2. Хорошее значение по
умолчанию — span = 0.75.
Рисунок 10 показывает, как span влияет на
приближение, выполненное функцией loess.
Заметьте, что меньшее значение span лучше
приближает флуктуации данных. Большее значение span
сглаживает колебания данных и создаёт более
гладкую приближающую функцию.
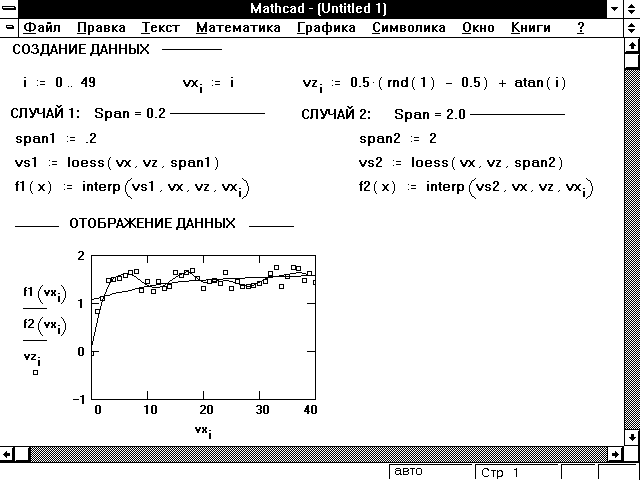
Рисунок 10: Влияние различных значений span на
функцию loess.
| egress (vx, vy, n) |
Возвращает вектор, требуемый interp,
чтобы найти полином порядка n, который
наилучшим образом приближает данные из vx и vy.
vx есть m-мерный вектор, содержащий
координаты x. vy есть m-мерный
вектор, содержащий координаты y
соответствующие m точкам, определенным в vx. |
| Е loess (vx, vy, span) |
Возвращает вектор, требуемый interp,
чтобы найти набор полиномов второго порядка,
которые наилучшим образом приближают
определённые окрестности выборочных точек,
определенных в векторах vx и vy. vx есть m-мерный
вектор, содержащий координаты x. vy - m-мерный
вектор, содержащий координаты y,
соответствующие m точкам, определенным в vx.
Аргумент span > 0) определяет, насколько
большие окрестности loess будет использовать
при выполнении локального приближения. |
| interp (vs, vx,
vy, x) |
Возвращает интерполируемое
значение y, соответствующее x. Вектор vs вычисляется
loess или regress на основе данных из vx и vy. |
Многомерная полиномиальная
регрессия
Функции loess и regress, обсужденные в
предыдущем разделе, также полезны, когда имеется
набор измеренных величин z, соответствующих
значениям x и y, и необходимо приблизить
полиномами поверхность, проходящую через эти
значения z.
Свойства этих функций описаны в предыдущем
разделе. При использовании этих функций для
приближения значений z, соответствующих двум
независимым переменным x и y, толкования
их аргументов должны быть изменены. А именно:
- Аргумент vx, который был m-мерным вектором
значений x, становится матрицей, состоящей из m
рядов и 2 столбцов, Mxy. Каждая строка Mxy
содержит x в первом столбце и соответствующее
значение y во втором столбце.
- Аргумент x для функции interp становится
двумерным вектором v, чьи элементы — значения
x и y, в которых нужно найти значение
полиномиальной функции, представляющей
наилучшее приближение данных из Mxy и vz.
| regress (Mxy,
vz, k) |
Возвращает вектор, требуемый interp,
чтобы найти полином k-ого порядка, который
наилучшим образом приближает данные из Mxy и vz.
Mxy есть m x 2 матрица, содержащая x-y
координаты. vz есть m-мерный вектор,
содержащий значения z, соответствующие
точкам, определенным в Mxy. |
| Е loess (Mxy, vz, span) |
Возвращает вектор, требуемый interp,
чтобы найти набор полиномов второго порядка,
которые наилучшим образом приближают
определённые окрестности выборочных точек,
определенных в массивах Mxy и vz. Mxy — m x 2
матрица, содержащая x-y координаты. vz — m
— мерный вектор, содержащий координаты z,
соответствующие m точкам, определенным в Mxy.
Аргумент span (span > 0) определяет, насколько
большую окрестность loess будет рассматривать
при выполнении локального приближения. |
| interp (vs, Mxy, vz,
v) |
Возвращает интерполируемое
значение z, соответствующее точке x = v0 и
y = v1. Вектор vs вычисляется ? loess или regress
на основе данных из Mxy и vz. |
Можно увеличивать число независимых
переменных, просто добавляя столбцы в массив Mxy,
а затем добавляя соответствующее число строк к
вектору v, который передается функции interp.
Функция regress может иметь любое число
независимых переменных. Но когда число
независимых переменных и степень полинома
больше четырёх, она будет работать медленнее и
требовать большего количества памяти. Функция loess
допускает максимум четыре независимых
переменных.
Имейте в виду, что для regress число значений
данных m должно удовлетворять соотношению
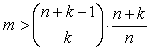
где n — число независимых переменных
(следовательно, число столбцов в Mxy), k —
желаемая степень полинома, и m — число
значений данных (следовательно, число строк в vz).
Например, если имеется пять независимых
переменных, и ищется приближение полиномом
четвёртой степени, потребуется более чем 126
наблюдений.
Обобщенная регрессия
К сожалению, линейная или полиномиальная
функции не во всех случаях подходят для описания
зависимости данных. Бывает, что нужно искать эту
зависимость в виде линейных комбинаций
произвольных функций, ни одна из которых не
является полиномом. Например, в рядах Фурье
следует аппроксимировать данные, используя
линейную комбинацию комплексных экспонент. Или
предполагается, что данные могут быть
смоделированы в виде линейной комбинации
полиномов Лежандра, но только неизвестно, какие
необходимо взять коэффициенты.
Функция linfit разработана, чтобы решить эти
виды проблем. Если предполагается, что данные
могли бы быть смоделированы в виде линейной
комбинации произвольных функций
y = a0 f0(x)
+ a1 f0(x)
+ a1 f1(x)
+...+ an f1(x)
+...+ an fn(x) fn(x)
следует использовать linfit, чтобы вычислить ai.
Рисунок 11 показывает пример, в котором линейная
комбинация трех функций: x, x2 и (x
+ 1)-1 используется для моделирования
некоторых данных.
Всё-таки имеются случаи, когда гибкость linfit
недостаточна — данные должны быть смоделированы
не линейной комбинацией данных, а некоторой
функцией, чьи параметры должны быть выбраны.
Например, если данные могут быть смоделированы в
виде суммы
f(x) = a1 sin(2x) + a2 sin(2x) + a2 tanh(3x) tanh(3x)
и всё, что нужно сделать — решить уравнение
относительно неизвестных коэффициентов a1
и a2, значит эта проблема решается с помощью linfit.
В противоположность этому, если данные должны
быть смоделированы в виде суммы
f(x) = 2 sin(a1x)
+ 3 sin(a1x)
+ 3 tanh(a2x) tanh(a2x)
и требуется найти неизвестные параметры a1
и a2, то это задача для функции genfit.
| linfit (vx, vy, F) |
Возвращает вектор, содержащий
коэффициенты, используемые, чтобы создать
линейную комбинацию функций из F, дающую
наилучшую аппроксимацию данных из векторов vx
и vy. F — функция, которая возвращает
вектор, состоящий из функций, которые нужно
oбъединить в виде линейной комбинации. |
| Е genfit (vx, vy, vg, F) |
Возвращает вектор, содержащий n
параметров u0, u1,...un-1, которые
обеспечивают наилучшее приближение данных из vx
и vy функцией f, зависящей от x и
параметров u0, u1,...un-1. F —
функция, которая возвращает n+1-мерный вектор,
содержащий f и ее частные производные
относительно параметров. vg есть n-мерный
вектор начальных значений для n параметров. |
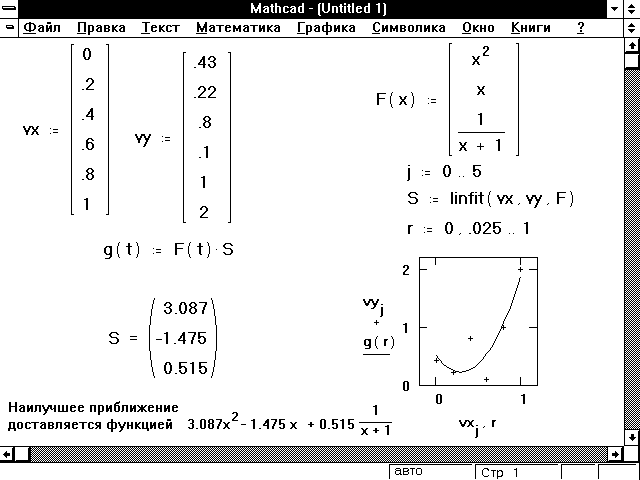
Рисунок 11: Использование linfit для нахождения
коэффициентов в линейной комбинации функций,
приближающей данные наилучшим образом.
Всё, что можно делать с помощью linfit, можно
также делать, хотя и менее удобно, с genfit.
Различие между этими двумя функциями есть
различие между решением системы линейных
уравнений и решением системы нелинейных
уравнений. Первая задача легко решается методами
линейной алгебры. Вторая задача гораздо более
трудная и решается итеративными методами. Это
объясняет, почему genfit нуждается в векторе
начальных значений в качестве аргумента, а linfit
в этом не нуждается.
Рисунок 12 показывает пример, в котором genfit
используется, чтобы найти экспоненту,
приближающую набор данных наилучшим образом.
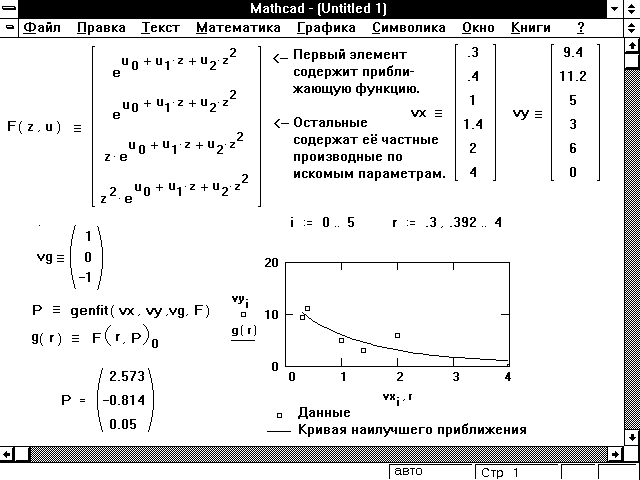
Рисунок 12: Использование genfit для нахождения
параметров функции, доставляющих ей наилучшее
приближение к данным.
  
|

