  Mathcad
использует несколько функций для работы с
распространёнными плотностями вероятности. Эти
функции распадаются на три класса:
- Плотности распределения вероятности:
вероятность того, что случайная величина будет
находиться в окрестности определённой точки,
пропорциональна плотности распределения
вероятности случайной величины в этой точке.
- Функции распределения (вероятности): они дают
вероятность, что случайная величина будет
принимать значение, меньшее или равное
определенной величине. Они получены просто
интегрированием (или суммированием, когда это
необходимо) соответствующей плотности
вероятности по подходящему интервалу значений.
- Обращения функций распределения: они позволяют
по заданной вероятности вычислить такое
значение, что вероятность того, что случайная
величина будет меньше или равна этому
значению, будет равна вероятности, заданной в
качестве аргумента.
Mathcad PLUS поставляется со всеми функциями,
перечисленными в следующих трех разделах. Если
Вы не используете Mathcad PLUS, Вы будете иметь все
функции, связанные со следующими законами
распределения вероятности: нормальным, хи-
квадрат, t-распределением Стьюдента, F,
биномиальным, Пуассона и равномерным.
Плотности распределения вероятности
Эти функции показывают отношение вероятности
того, что случайная величина попадает в малый
диапазон значений с центром в заданной точке, к
величине этого диапазона. Функции плотности
вероятности — производные соответствующих
функций распределения, обсуждаемых в следующем
разделе.
| Е
dbeta(x, s1, s2) |
Возвращает плотность
вероятности бэта-распределения: 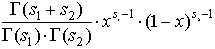
где (s1, s2 >0) являются
параметрами формы. (0 < x < 1). |
| dbinom(k,
n, p) |
Возвращает P(X = k), когда
случайная величина X имеет биномиальное
распределение: 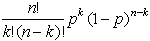
в котором n и k являются целыми
числами, удовлетворяющими условию 0 k< k< n. р удовлетворяет 0 n. р удовлетворяет 0 p p 1. 1. |
| Е
dcauchy(x, l, s) |
Возвращает плотность
вероятности распределения Коши: (p s(1 + ((x - l)/s)2))-1
в котором l
является параметром расположения, а
s>0 есть параметр масштаба. |
| dchisq(x,
d) |
Возвращает плотность
вероятности для хи-квадрат распределения: 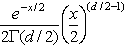
в котором d>0 является числом степеней
свободы, и x>0. |
| Е
dexp(x, r) |
Возвращает плотность
вероятности экспоненциального распределения: re-rx
в котором r>0 является параметром, и x>0. |
| dF(x, d1,
d2 ) |
Возвращает плотность
вероятности F-распределения : 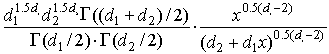
в котором d1, d2>0
являются числами степеней свободы и x>0. |
| Е
dgamma(x, s) |
Возвращает плотность
вероятности Гамма -распределения: 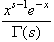
в котором s>0 является параметром формы,
и x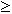 0. 0. |
| Е
dgeom(k, p) |
Возвращает , когда
случайная величина X подчиняется
геометрическому распределению p(1
- p)k
в котором 0 < p  1является вероятностью успеха
в отдельном испытании, k есть
неотрицательное целое число. 1является вероятностью успеха
в отдельном испытании, k есть
неотрицательное целое число. |
| Е
dlnorm(x, m, s) |
Возвращает плотность
вероятности логнормального распределения: 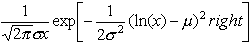
в котором m равно
натуральному логарифму среднего значения, s>0 равно натуральному
логарифму среднеквадратичного отклонения, и x>0. |
| Е
dlogis(x, l, s) |
Возвращает плотность
вероятности логистического распределения: 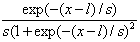
в котором l является параметром
расположения, и s >0 есть параметр
масштаба. |
| Е
dnbinom(k, n, p) |
Возвращает P(X = k), когда
случайная величина X имеет отрицательное
биномиальное распределение: 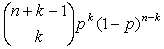
в котором 0 < p  1, а
n и k являются целыми числами, n > 0 и
k 1, а
n и k являются целыми числами, n > 0 и
k 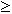 0. 0. |
| dnorm(x,
m, s) |
Возвращает плотность
вероятности нормального распределения: 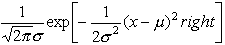
в котором m и s есть среднее значение и
среднеквадратичное отклонение. s
> 0. |
| dpois(k,
l) |
Возвращает P(X = k), когда
случайная величина X имеет распределение
Пуассона: 
в котором l > 0, а k
является неотрицательным целым числом. |
| dt(x, d) |
Вычисляет плотность
вероятности t -распределения
Стьюдента: 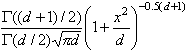 , ,
в котором d является числом степеней
свободы, d > 0 , а x есть вещественное
число. |
| dunif(x,
a, b) |
Вычисляет плотность
вероятности равномерного распределения: 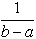 , ,
в котором b и a являются
граничными точками интервала, a < b
и a  x x  b . b . |
| Е
dweibull(x, s) |
Вычисляет плотность
вероятности распределения Вейбулла: sxs-1exp(-xs)
в котором s > 0 есть параметр формы и x
> 0. |
Эти функции возвращают вероятность того, что
случайная величина меньше или равна
определенному значению. Функция распределения
вероятности — просто функция плотности
вероятности, проинтегрированная от - до определенного
значения. Для целочисленных случайных величин
интеграл заменен суммированием по
соответствующим индексам. до определенного
значения. Для целочисленных случайных величин
интеграл заменен суммированием по
соответствующим индексам.
Рисунок 1 в конце этого раздела иллюстрирует
связь между плотностью вероятности и функцией
распределения случайной величины.
| cnorm (x) |
Возвращает стандартную
нормальную функцию распределения. Эквивалент pnorm
(x, 0, 1). |
| Е
pbeta (x, s1, s2) |
Возвращает функцию
бэта-распределения с параметрами формы s1
и s2. ( s1, s2 > 0). |
| pbinom (k, n, p)
|
Возвращает функцию
биномиального распределения для k успехов в n
испытаниях. n есть натуральное число. p
есть вероятность успеха, 0 p p 1. 1. |
| Е
pcauchy (x, l, s) |
Возвращает функцию
распределения Коши с параметром масштаба s и
параметром расположения l. s > 0. |
| pchisq (x, d) |
Возвращает функцию
распределения хи-квадрат, в котором d > 0
равно числу степеней свободы. |
| Е
pexp (x, r) |
Возвращает функцию
экспоненциального распределения, в котором r
> 0 является параметром. |
| pF (x, d1,
d2) |
Возвращает функцию
F-распределения, в котором d1, d2 >
0 являются числами степеней свободы. |
| Е
pgamma (x, s) |
Возвращает функцию
Гамма-распределения, в котором s > 0
является параметром формы. |
| Е
pgeom (k, p) |
Возвращает функцию
геометрического распределения. p есть
вероятность успеха в одиночном испытании. 0 < p  1. 1. |
| Е
plnorm (x, m, s) |
Возвращает функцию
логнормального распределения, в котором m равно логарифму среднего
значения, а s > 0 есть
логарифм среднеквадратичного отклонения. |
| Е
plogis (x, l, s) |
Возвращает функцию
логистического распределения. l есть
параметр расположения.s > 0 - параметр
масштаба. |
| Е
pnbinom (k, n, p) |
Возвращает функцию
отрицательного биномиального распределения, в
котором 0 < p  1. n
— натуральное. 1. n
— натуральное. |
| pnorm (x, m, s) |
Возвращает функцию нормального
распределения со средним m
и среднеквадратичным отклонением s. s > 0. |
| ppois (k, l) |
Возвращает функцию
распределения Пуассона. l > 0. |
| pt (x, d) |
Возвращает функцию t-распределения
Стьюдента. d есть число степеней свободы. d
> 0. |
| punif (x, a, b) |
Возвращает функцию равномерного
распределения. b и a есть граничные точки
интервала. a < b . |
| Е
pweibull (x, s) |
Возвращает функцию
распределения Вейбулла. s > 0. |
Эти функции принимают вероятность p как
аргумент и возвращают значение x такое, что P(X
 x) = p. x) = p.
| Е qbeta (p, s1, s2) |
Обращает бета-распределение с
параметрами формы s1 и s2. (0 p p 1) (s1, s2
>0). 1) (s1, s2
>0). |
| qbinom (p, n, r) |
Возвращает число успехов в n
испытаниях схемы Бернулли при условии, что
вероятность успехов не превышает p и r —
вероятность успеха на одиночном испытании. 0  r r  1 и 0 1 и 0  p p  1. n есть натуральное число. 1. n есть натуральное число. |
| Е qcauchy (p, l, s) |
Обращает распределение Коши с
параметром масштаба s и параметром
расположения l. s > 0. 0< p<1. |
| qchisq (p, n) |
Обращает хи-квадрат
распределение, в котором d > 0
является числом степеней свободы. 0  p < 1. p < 1. |
| Е qexp (p, r) |
Обращает экспоненциальное
распределение, в котором r > 0
является параметром. 0  p < 1. p < 1. |
| qF (p, d1,
d2) |
Обращает F -распределение, в
котором d1, d2 >0 являются
числами степеней свободы. 0  p < 1. p < 1. |
| Е qgamma (p, s) |
Обращает Гамма-распределение, в
котором s > 0 является параметром формы. 0
 p < 1. p < 1. |
| Е qgeom (p, r) |
Обращает геометрическое
распределение. r - вероятность успеха при
одиночном испытании. 0 < p < 1 и 0 < r
< 1. |
| Е qlnorm (p, m, s) |
Обращает логнормальное
распределение, в котором m
является натуральным логарифмом среднего
значения, s > 0 - натуральный
логарифм среднеквадратичного отклонения. 0  p < 1. p < 1. |
| Е qlogis (p, l, s) |
Обращает логистическое
распределение. l — параметр расположения, s >
0 — параметр масштаба. 0 < p < 1. |
| Е qnbinom (p, n, r) |
Обращает отрицательное
биномиальное распределение с числом испытаний n
и вероятностью успеха в одиночном испытании r.
0 < r  1 и 0 1 и 0  p p  1. 1. |
| qnorm (p, m, s) |
Обращает нормальное
распределение со средним m
и среднеквадратичным отклонением s. 0 < p < 1 и s >
0. |
| qpois (p, l) |
Обращает распределение
Пуассона. l > 0 и 0  p p  1. 1. |
| qt (p, d) |
Обращает t-распределение
Стьюдента. d -число степеней свободы. d >
0 и 0 < p < 1. |
| qunif (p, a, b) |
Обращает равномерное
распределение. b и a — граничные точки
интервала. a < b и 0  p p  1. 1. |
| Е qweibull (p, s) |
Обращает распределение
Вейбулла. s > 0 и 0 < p < 1. |
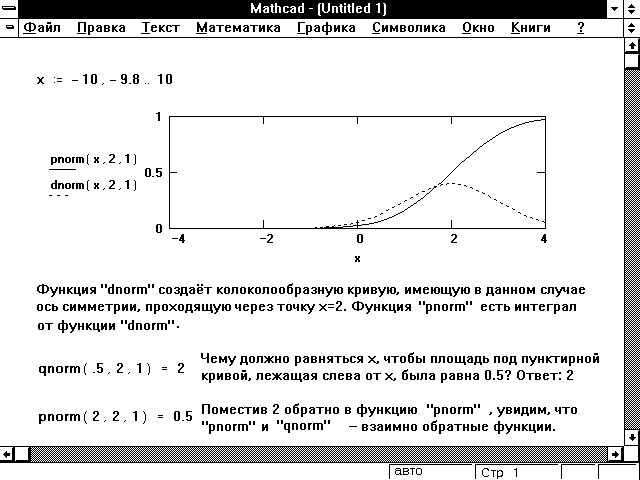
Рисунок 1: Связь между плотностями
вероятности, функциями распределения и их
обратными функциями.
  
|

