  Mathcad
дает возможность решать также и системы
уравнений. Максимальное число уравнений и
переменных равно пятидесяти. В первой части
этого раздела описаны процедуры решения систем
уравнений. В заключительной части приведены
примеры и проведено обсуждение некоторых часто
встречающихся ошибок. Результатом решения
системы будет численное значение искомого корня.
Для символьного решения уравнений необходимо
использовать блоки символьного решения
уравнений. При символьном решении уравнений
искомый корень выражается через другие
переменные и константы.
Для решения системы уравнений выполните
следующее:
- Задайте начальные приближения для всех
неизвестных, входящих в систему уравнений. Mathcad
решает уравнения при помощи итерационных
методов. На основе начального приближения
строится последовательность, сходящаяся к
искомому решению.
- Напечатайте ключевое слово Given. Оно
указывает Mathcad, что далее следует система
уравнений. При печати слова Given можно
использовать любой шрифт, прописные и строчные
буквы. Убедитесь, что при этом Вы не находитесь в
текстовой области или параграфе.
- Введите уравнения и неравенства в любом порядке
ниже ключевого слова Given. Удостоверьтесь, что
между левыми и правыми частями уравнений стоит
символ =. Используйте [Ctrl]= для печати
символа =. Между левыми и правыми частями
неравенств может стоять любой из символов <,
>,
 , и , и 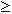 . .
- Введите любое выражение, которое включает
функцию Find. При печати слова Find можно
использовать шрифт любого размера, произвольный
стиль, прописные и строчные буквы.
| Find(z1, z2, z3, . .
. ) |
Возвращает решение системы
уравнений. Число аргументов должно быть равно
числу неизвестных. |
Функция Find возвращает найденное
решение следующим образом:
- Если функция Find имеет только один аргумент,
то она возвращает решение уравнения,
расположенного между ключевым словом Given и
функцией Find.
- Если функция Find имеет более одного
аргумента, то она возвращает ответ в виде
вектора. Например, Find(z1, z2) возвращает
вектор, содержащий значения z1 и z2 ,
являющиеся решением системы уравнений.
Ключевое слово Given, уравнения и неравенства,
которые следуют за ним, и какое-либо выражение,
содержащее функцию Find, называются блоком
решения уравнений.
На Рисунке 5 показан рабочий документ, который
использует блок решения уравнений для решения
одного уравнения с одним неизвестным. Так как
имеется только одно уравнение, то только одно
уравнение появляется между ключевым словом Given
и формулой, включающей функцию Find. Так как
уравнение имеет одно неизвестное, то функция Find
имеет только один аргумент. Для решения одного
уравнения с одним неизвестным можно также
использовать функцию root, как показано ниже:
a := root(x2 + 10 - ex , x)

Рисунок 5: Блок решения уравнений для одного
уравнения с одним неизвестным.
Между ключевым словом Given и функцией Find в
блоке решения уравнений могут появляться
выражения строго определенного типа. Ниже
приведен список всех выражений, которые могут
быть использованы в блоке решения уравнений.
Использование других выражений не допускается.
Эти выражения часто называются ограничениями. В
таблице, приведенной ниже, через x и y
обозначены вещественнозначные скалярные
выражения, а через z и w обозначены любые
скалярные выражения.
| Условие |
Как ввести |
Описание |
| w = z |
[Ctrl] = |
Булево равенство возвращает 1,
если операнды равны; иначе 0 |
| x > y |
> |
Больше чем. |
| x < y |
< |
Меньше чем. |
x 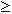 y y |
[Ctrl]0 |
Больше либо равно. |
x  y y |
[Ctrl]9 |
Меньше либо равно. |
w 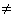 z z |
[Ctrl]3 |
Не равно. |
Следующие выражения недопустимы
внутри блока решения уравнений:
- Ограничения со знаком
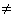 . .
- Дискретный аргумент или выражения, содержащие
дискретный аргумент в любой форме.
- Неравенства вида a < b < c.
Если необходимо включить полученный в блоке
решения уравнений результат в итерационный
процесс, обратитесь к разделу “Как
лучше искать корни,” который находится ниже в
этой главе.

Рисунок 6: Блок решения уравнений для системы из
двух уравнений с двумя неизвестными и
ограничениями на переменные в виде неравенств.
Блоки решения уравнений не могут быть вложены
друг в друга. Каждый блок решения уравнений может
иметь только одно ключевое слово Given и имя
функции Find. Можно, однако, определить функцию f(x)
:= Find(x) в конце одного блока решения уравнений и
затем использовать f(x) в другом блоке. Эта
возможность также обсуждена в разделе “Как лучше искать корни” ниже в
этой главе.
Как правило, нельзя использовать оператор
присваивания (выражения вида x:=1) внутри блока
решения уравнений. Mathcad помечает операторы
присваивания, которые находятся внутри блока
решения уравнений, сообщением об ошибке.
На Рисунке 6 показан блок решения уравнений, в
котором использованы некоторые виды ограничений
на искомое решение. Решаются два уравнения с
двумя неизвестными. В результате функция Find
содержит два аргумента, x и y, и возвращает
ответ в виде вектора с двумя компонентами.
Как использовать найденное решение
Функция Find, которая завершает блок решения
уравнений, может быть использована аналогично
любой другой функции. Можно произвести с этой
функцией следующие три действия:
- Можно вывести найденное решение, напечатав
выражение вида Find(variable) =. Пример приведен в
верхней половине Рисунка 7. Если
решаются уравнения с несколькими неизвестными,
то можно вывести вектор результатов, введя
выражение вида Find(vari1, var2,...) =. Пример
того, как это делается для системы двух уравнений
с двумя неизвестными, приведен на Рисунке 8.
- Можно определить переменную с использованием
этой функции. Для этого в конце блока решения
уравнений необходимо ввести выражение a := Find(x).
Это удобно сделать, если требуется использовать
решение системы уравнений в другом месте
рабочего документа. Как только переменная a определена
таким образом, она сразу же принимает значение
искомого корня. Пример, иллюстрирующий такую
возможность, приведен в нижней половине Рисунка
7. Если функция Find возвращает вектор значений,
можно ввести выражение variable := Find(vari1, var2,...).
После такого определения переменная становится
вектором (вместо скаляра). Можно также определить
переменные, как показано на Рисунке 6.
- Используя Find, можно определить другую
функцию. Для этого необходимо закончить блок
решения уравнений выражением типа f(a, b, c,...)
:= Find(x, y, z,...). Эта конструкция
удобна при многократном решении системы
уравнений для различных значений некоторых
параметров a, b, с, . . ., непосредственно
входящих в систему уравнений. Эта методика
описана в разделе “Как лучше
искать корни” ниже в этой главе.

Рисунок 7: Можно отобразить результат,
полученный в блоке решения уравнений,
непосредственно либо присвоить его переменной
для дальнейшего использования.

Рисунок 8: При решении системы уравнений с двумя
или большим числом неизвестных функция Find
возвращает вектор, имеющий число компонент,
равное числу неизвестных.
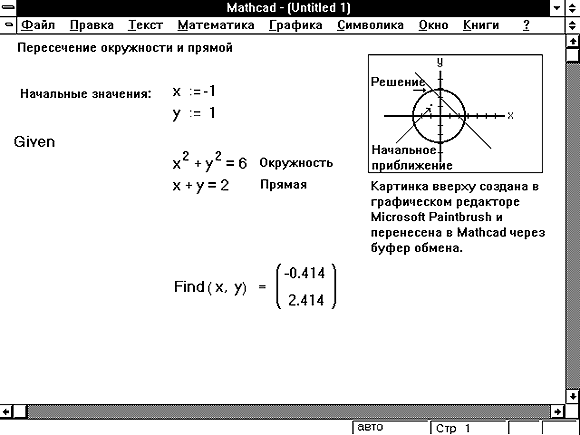
Рисунок 9: Различные начальные приближения
приводят к различным решениям. Получено решение,
отличное от решения, приведенного на Рисунке 8.
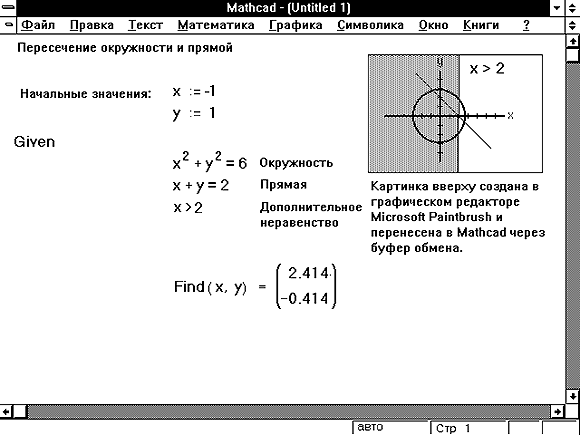
Рисунок 10: Добавление ограничений позволяет
найти другое решение.
Mathcad возвращает в блоке решения уравнений
только одно решение. Однако система уравнений
может иметь несколько различных решений. Если
одно из решений найдено, то для поиска других
решений можно использовать различные начальные
приближения либо дополнительные ограничения в
виде неравенств, которым найденное решение не
удовлетворяет. На Рисунке 9 показано, как иное
начальное приближение может приводить к другому
решению задачи, приведенной на Рисунке 8. На
Рисунке 10 показано, как добавить ограничения в
виде неравенства для поиска другого решения.
Что делать, когда Mathcad не может найти решения
Если в результате решения уравнений на
каком-либо шаге итераций не может быть найдено
более приемлемое приближение к искомому решению
по сравнению с предыдущим шагом, то поиск решения
прекращается, а функция Find помечается
сообщением об ошибке “решение не найдено”.
Если при поиске решения встречаются трудности,
то полезно вывести те или иные графики, связанные
с системой. Анализ графика может облегчить поиск
области, в которой может находиться искомое
решение. Это поможет выбрать подходящее
начальное приближение.
На Рисунке 11 приведена задача, для которой Mathcad
не смог найти решение.
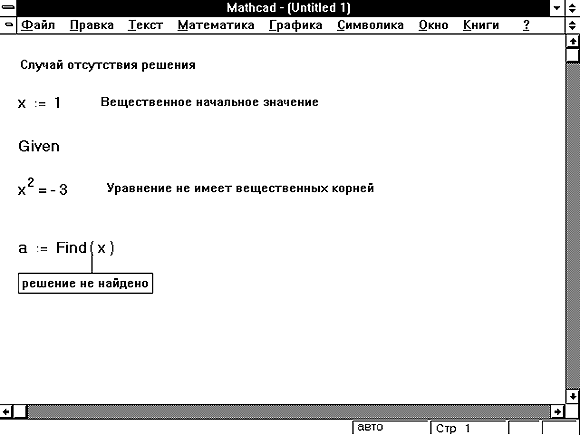
Рисунок 11: Пример задачи, решение которой не
может быть найдено в блоке решения уравнений.
Сообщение об ошибках “решение не найдено”
при решении уравнений появляется, когда различие
между текущим приближением и приближением,
полученным на предыдущем шаге итераций, больше,
чем значение встроенной переменной TOL, и выполнено
одно из следующих условий:
- Достигнута точка, из которой не может быть
получено более точное приближение к решению.
- Достигнута точка, из которой невозможно выбрать
подходящее направление спуска — направление
вдоль которого ищется следующее приближение. В
связи с этим продолжать итерации невозможно.
- Достигнут предел точности вычислений.
Дальнейшие вычисления не увеличивают точность
найденного решения вследствие влияния ошибок
округления. Это часто случается, если
установлено значение встроенной переменной TOL
меньшее, чем 10-15.
Причиной появления этого сообщения об ошибке
может быть следующее:
- Поставленная задача может не иметь решения.
- Для уравнения, которое не имеет вещественных
решений, в качестве начального приближения взято
вещественное число. Если решение задачи
комплексное, то оно не будет найдено, если только
в качестве начального приближения не взято также
комплексное число. На Рисунке 11 приведен
соответствующий пример.
- В процессе поиска решения последовательность
приближений попала в точку локального минимума
невязки. Метод поиска решения, который
используется в Mathcad, не позволяет в этом случае
построить следующее приближение, которое бы
уменьшало невязку. Для поиска искомого решения
пробуйте использовать различные начальные
приближения или добавьте ограничения на
переменные в виде неравенств, чтобы обойти точку
локального минимума.
- В процессе поиска решения получена точка,
которая не является точкой локального минимума,
но из которой метод минимизации не может
определить дальнейшее направление движения.
Метод преодоления этой проблемы — такой же, как
для точки локального минимума: измените
начальное приближение или добавьте ограничения
в виде неравенств, чтобы миновать нежелательную
точку остановки.
- Возможно, поставленная задача не может быть
решена с заданной точностью. Если значение
встроенной переменной TOL слишком мало, то Mathcad
может достигнуть точки, находящейся достаточно
близко к решению задачи, но уравнения и
ограничения при этом не будут выполнены с
точностью, задаваемой переменной TOL. Попробуйте
увеличить значение TOL где-нибудь выше блока
решения уравнений.
Что делать, когда имеется слишком мало
ограничений
Если количество ограничений меньше, чем
количество переменных, Mathcad вообще не может
выполнить блок решения уравнений. Mathcad помечает в
этом случае функцию Find сообщением об ошибке “слишком
мало ограничений”.
Задача, аналогичная той, которая приведена на
Рисунке 12, называется недоопределенной.
Ограничений в ней меньше, чем переменных. Поэтому
ограничения не содержат достаточной информации
для поиска решения. Поскольку функция Find
имеет пять аргументов, Mathcad определяет, что
требуется решить два уравнения с пятью
неизвестными. Вообще говоря, такая задача обычно
имеет бесконечное число решений.
При использовании блока решения уравнений в
Mathcad необходимо задать количество уравнений по
крайней мере не меньшее, чем число искомых
неизвестных. Если зафиксировать значения
некоторых переменных, удастся решить уравнения
относительно оставшихся переменных. На Рисунке 13
показано, как, зафиксировав часть переменных,
решить недоопределенную задачу из Рисунка 12.
Поскольку функция Find содержит только два
аргумента, z и w, Mathcad определяет
переменные x, y и v как имеющие
фиксированные значения 10, 50 и 0 соответственно.
Блок решения уравнений становится в этом случае
корректно определенным, потому что теперь
имеются только две неизвестных, z и w, и два
уравнения.

Рисунок 12: Функция Find имеет пять аргументов,
поэтому Mathcad определяет, что требуется решить два
уравнения с пятью неизвестными.

Рисунок 13: Проблема может быть решена, если
уменьшить количество аргументов функции Find.
  
|

