  Mathcad содержит функции для
обычных в линейной алгебре действий с массивами.
Эти функции предназначены для использования с
векторами и матрицами. Если явно не указано, что
функция определена для векторного или
матричного аргумента, не следует в ней
использовать массивы как аргумент. Обратите
внимание, что операторы, которые ожидают в
качестве аргумента вектор, всегда ожидают
вектор-столбец, а не вектор-строку. Чтобы
заменить вектор-строку на вектор-столбец,
используйте оператор транспонирования [Ctrl]1. Mathcad содержит функции для
обычных в линейной алгебре действий с массивами.
Эти функции предназначены для использования с
векторами и матрицами. Если явно не указано, что
функция определена для векторного или
матричного аргумента, не следует в ней
использовать массивы как аргумент. Обратите
внимание, что операторы, которые ожидают в
качестве аргумента вектор, всегда ожидают
вектор-столбец, а не вектор-строку. Чтобы
заменить вектор-строку на вектор-столбец,
используйте оператор транспонирования [Ctrl]1.
Если Вы используете Mathcad PLUS, Вы будете также
иметь несколько дополнительных функций,
определенных для векторов. Эти функции скорее
предназначены для анализа данных, чем для
действий с матрицами. Они обсуждены в Главе “Встроенные функции”.
Следующие таблицы перечисляют векторные и
матричные функции Mathcad. В этих таблицах
- A
и B — массивы (векторы или матрицы).
- v
— вектор.
- M
и N — квадратные матрицы.
- z
— скалярное выражение.
- Имена, начинающиеся с букв m, n, i или j —
целые числа.
Размеры и диапазон значений массива
В Mathcad есть несколько функций, которые
возвращают информацию относительно размеров
массива и диапазона его элементов. Рисунок 10
показывает, как эти функции используются.
| Имя функции |
Возвращается... |
| rows(A) |
Число строк в массиве A. Если А
— скаляр, возвращается 0. |
| cols(A) |
Число столбцов в массиве A.
Если A скаляр, возвращается 0. |
| length(v) |
Число элементов в векторе v. |
| last(v) |
Индекс последнего элемента в
векторе v. |
| max(A) |
Самый большой элемент в массиве A.
Если A имеет комплексные элементы, возвращает
наибольшую вещественную часть плюс i, умноженную
на наибольшую мнимую часть. |
| min(A) |
Самый маленький элемент в
массиве A. Если A имеет комплексные
элементы, возвращает наименьшую вещественную
часть плюс i, умноженную на наименьшую мнимую
часть. |

Рисунок 10: Векторные
и матричные функции для нахождения размера
массива и получения информации относительно
диапазона элементов.
Специальные типы матриц
Можно использовать следующие функции, чтобы
произвести от массива или скаляра матрицу
специального типа или формы. Функции rref, diag и geninv
доступны только в Mathcad PLUS.
| Имя функции |
Возвращается... |
| identity(n)
|
n x n единичная матрица (матрица,
все диагональные элементы которой равны 1, а все
остальные элементы равны 0). |
| Re(A) |
Массив, состоящий из элементов,
которые являются вещественными частями
элементов A. |
| Im(A) |
Массив, состоящий из элементов,
которые являются мнимыми частями элементов A. |
| Е
diag(v) |
Диагональная матрица,
содержащая на диагонали элементы v. |
| Е
geninv(A) |
Левая обратная к A матрица L
такая, что L A = I, где I -
единичная матрица, имеющая то же самое число
столбцов, что и A. Матрица А - m x n вещественная
матрица, где m>=n. A = I, где I -
единичная матрица, имеющая то же самое число
столбцов, что и A. Матрица А - m x n вещественная
матрица, где m>=n. |
| Е
rref(A) |
Ступенчатая форма матрицы A. |

Рисунок 11: Функции для
преобразования массивов. Обратите внимание, что
функции diag и rref являются доступными только в Mathcad PLUS.
Специальные характеристики матрицы
Можно использовать функции из следующей
таблицы, чтобы найти след, ранг, нормы и числа
обусловленности матрицы. Кроме tr, все эти
функции доступны только в Mathcad PLUS.
| Имя функции |
Возвращается... |
| tr(M) |
Сумма диагональных элементов,
называемая следом M. |
| Е
rank(A) |
Ранг вещественной матрицы A. |
| Е norm1(M) |
L1 норма матрицы M. |
| Е norm2(M) |
L2 норма матрицы M. |
| Е norme(M) |
Евклидова норма матрицы M. |
| Е normi(M) |
Равномерная норма матрицы M. |
| Е cond1(M) |
Число обусловленности матрицы M,
основанное на L1 норме. |
| Е cond2(M) |
Число обусловленности матрицы M,
основанное на L2 норме. |
| Е conde(M) |
Число обусловленности матрицы M,
основанное на евклидовой норме. |
| Е condi (M) |
Число обусловленности матрицы
M, основанное на равномерной норме. |
В Mathcad есть две функции для объединения матриц
вместе — бок о бок, или одна над другой. В Mathcad
также есть функция для извлечения подматрицы.
Рисунки 12 и 13 показывают некоторые примеры.
| Имя функции |
Возвращается... |
| augment (A,
B) |
Массив, сформированный
расположением A и B бок о бок.
Массивы A и B должны иметь
одинаковое число строк. |
| stack (A,
B) |
Массив, сформированный
расположением A над B. Массивы A
и B должны иметь одинаковое число
столбцов. |
| submatrix
(A, ir, jr, ic, jc) |
Субматрица, состоящая из всех
элементов, содержащихся в строках с ir по jc
и столбцах с ic по jc. Чтобы поддерживать
порядок строк и-или столбцов, удостоверьтесь, что
ir<=jr и ic<=jc, иначе
порядок строк и-или столбцов будет обращен. |
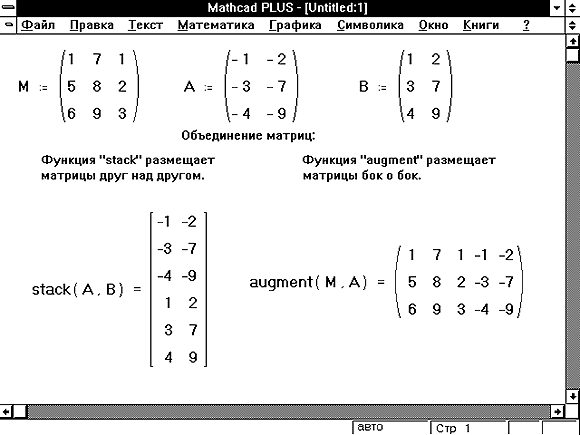
Рисунок 12: Объединение матриц функциями stack и
augment.

Рисунок 13: Извлечение субматрицы из матрицы при
помощи функции submatrix.
Собственные значения и собственные векторы
В Mathcad существуют функции eigenval и eigenvec для
нахождения собственных значений и собственных
векторов матрицы. В Mathcad PLUS также есть функция eigenvecs
для получения всех собственных векторов сразу.
Если Вы используете Mathcad PLUS, Вы будете также иметь
доступ к genvals и genvecs для нахождения
обобщенных собственных значений и собственных
векторов. Рисунок 14 показывает, как некоторые из
этих функций используются.
| Имя функции |
Возвращается... |
| eigenvals
(M) |
Вектор, содержащий собственные
значения матрицы M. |
| eigenvec
(M, z) |
Матрица, содержащая
нормированный собственный вектор,
соответствующий собственному значению z
квадратной матрицы M. |
| Е
eigenvecs (M) |
Матрица, содержащая
нормированные собственные векторы,
соответствующие собственным значениям
квадратной матрицы M. n-ный столбец
возвращенной матрицы — собственный вектор,
соответствующий n-ному собственному
значению, возвращенному eigenvals. |
| Е
genvals (M,N) |
Вектор v собственных значений,
каждое из которых удовлетворяет обобщенной
задаче о собственных значениях . Матрицы M и N
— вещественнозначные квадратные матрицы одного
размера. Вектор x — соответствующий
собственный вектор. |
| Е
genvecs (M,N) |
Матрица, содержащая
нормализованные собственные векторы,
соответствующие собственным значениям в v,
векторе, возвращенном genvals. n-ный столбец
этой матрицы — собственный вектор x,
удовлетворяющий обобщенной задаче о собственных
значениях . Матрицы M и N —
вещественнозначные квадратные матрицы одного
размера. |

Рисунок 14: Нахождение собственных значений
и собственных векторов.

Рисунок 15: Использование eigenvecs для
одновременного нахождения всех собственных
векторов.
Разложения
Если Вы используете Mathcad PLUS, Вы будете иметь
доступ к некоторым дополнительным функциям для
выполнения специальных разложений матрицы: QR, LU,
Холесского, и по сингулярным базисам. Некоторые
из этих функций возвращают две или три матрицы,
соединенные вместе в одну большую матрицу.
Используйте submatrix, чтобы извлечь эти две или
три меньшие матрицы. Рисунок 16 показывает пример.
| Имя функции |
Возвращается... |
| Е
cholesky(M) |
Нижняя треугольная матрица L
такая, что L LT=M.
Матрица M должна быть симметричной
положительно определенной. Симметрия означает,
что M=MT, положительная
определённость — что xT LT=M.
Матрица M должна быть симметричной
положительно определенной. Симметрия означает,
что M=MT, положительная
определённость — что xT M M x>0
для любого вектора x x>0
для любого вектора x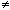 0. 0. |
| Е
qr(A) |
Матрица, чьи первые n
столбцов содержат ортогональную матрицу Q, а
последующие столбцы содержат верхнюю
треугольную матрицу R. Матрицы Q и R
удовлетворяют равенству A=Q R. Матрица A должна быть
вещественной. R. Матрица A должна быть
вещественной. |
| Е
lu(M) |
Матрица, которая содержит три
квадратные матрицы P, L и U, расположенные
последовательно в указанном порядке и имеющие с M
одинаковый размер. L и U являются
соответственно нижней и верхней треугольными
матрицами. Эти три матрицы удовлетворяют
равенству P M=L M=L U . U . |
| Е
svd(A) |
Матрица, содержащая две
расположенные друг над другом матрицы U и V.
Сверху находится U — размера m x n, снизу V —
размера n x n. Матрицы U и V удовлетворяют
равенству A=U diag(s) diag(s) VT, где s
— вектор, возвращенный svds(A). A должна быть
вещественнозначной матрицей размера m x n, где
m>=n. VT, где s
— вектор, возвращенный svds(A). A должна быть
вещественнозначной матрицей размера m x n, где
m>=n. |
| Е
svds(A) |
Вектор, содержащий сингулярные
значения вещественнозначной матрицы размера m x n,
где m>=n. |
Рисунок 16: Использование функции submatrix для
извлечения результата из функции rq. Используйте
submatrix, чтобы извлечь подобным образом результаты
из функций lu и svd. Обратите внимание, что эти
функции доступны только в Mathcad PLUS.
Решение линейной системы уравнений
Если Вы используете Mathcad PLUS, Вы сможете
использовать функцию lsolve для решения
линейной системы уравнений. Рисунок 17 показывает
пример. Обратите внимание, что M не может быть
ни вырожденной, ни почти вырожденной для
использования с lsolve. Матрица называется
вырожденной, если её детерминант равен нулю.
Матрица почти вырождена, если у неё большое число
обусловленности. Можно использовать одну из
функций, описанных на странице 204, чтобы найти
число обусловленности матрицы.
| Имя функции |
Возвращается... |
| Е
lsolve (M, v) |
Вектор решения x такой,
что M x=v. x=v. |

Рисунок 17: Использование lsolve для решения
системы из двух уравнений с двумя неизвестными.
  
|

