  Любое вычисление, которое
Mathcad может выполнять с одиночными значениями, он
может также выполнять с векторами или матрицами
значений. Есть два способа сделать это: Любое вычисление, которое
Mathcad может выполнять с одиночными значениями, он
может также выполнять с векторами или матрицами
значений. Есть два способа сделать это:
- Последовательно выполняя вычисления над каждым
элементом с использованием дискретного
аргумента, как описано в следующей главе “Дискретные аргументы”.
- Используя оператор векторизации, описанный в
этой главе.
Оператор векторизации предписывает Mathcad
выполнить одну и ту же операцию над каждым
элементом вектора или матрицы.
Математическая запись часто указывает на
многократность операции, используя нижние
индексы. Вот как определяется матрица P,
получаемая перемножением соответствующих
элементов матриц M и N:
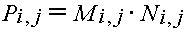
Обратите внимание, что это не умножение матриц,
но поэлементное перемножение. Mathcad позволяет
выполнить эту операцию с использованием
нижних индексов, как описано в следующей главе,
но намного проще использовать векторизованное
равенство.
Как применять оператор векторизации к
выражению
Вот как применить оператор векторизации к
выражению подобному М N: N:
- Выделите выражение целиком, щёлкнув внутри и
нажимая [], пока оно не
окажется заключенным в выделяющую рамку.
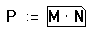
- Нажмите [Ctrl], чтобы применить оператор
векторизации. Mathcad помещает стрелку сверху
выделенного выражения.
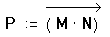
Как оператор векторизации изменяет смысл
выражения.
Оператор векторизации изменяет смысл
операторов и функций, к которым применяется.
Оператор векторизации предписывает Mathcad
применять операторы и функции в их скалярном
значении к каждому элементу массива поочередно.
Ниже приводятся некоторые примеры того, как
оператор векторизации изменяет смысл выражений
с векторами и матрицами:
- Если v — вектор, sin(v) — недопустимое
выражение. Но если используется оператор
векторизации, Mathcad вычисляет синус каждого
элемента v, результат — новый вектор, чьи
элементы — синусы элементов v.
- Если M — матрица,
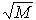 — недопустимое выражение. Но если
применяется оператор векторизации, Mathcad
вычисляет квадратный корень каждого элемента M и
помещает результаты в новой матрице. — недопустимое выражение. Но если
применяется оператор векторизации, Mathcad
вычисляет квадратный корень каждого элемента M и
помещает результаты в новой матрице.
- Если v и w — векторы, то v
 w означает скалярное
произведение v и w. Но если применяется
оператор векторизации, результат — новый вектор,
чей i-ный элемент получен перемножением vi
и wi. Это не то же самое, что скалярное
произведение. w означает скалярное
произведение v и w. Но если применяется
оператор векторизации, результат — новый вектор,
чей i-ный элемент получен перемножением vi
и wi. Это не то же самое, что скалярное
произведение.
Эти свойства оператора векторизации позволяют
использовать скалярные операторы и функции с
массивами. В настоящем руководстве это
называется “векторизацией” выражения.
Например, предположим, что нужно применять
формулу корней квадратного уравнения к трем
векторам, содержащим коэффициенты a, b и c.
Рисунок 18 показывает обычное использование этой
формулы. Рисунок 19 показывает, как использовать
её, когда a, b и c — векторы.

Рисунок 18: Формула корней квадратного
уравнения.

Рисунок 19: Формула корней квадратного
уравнения в применении к векторам.
Оператор векторизации появляется как стрелка
над формулой корней квадратного уравнения на
Рисунке 19. Его использование существенно в этом
вычислении. Без него Mathcad интерпретировал бы a c как скалярное
произведение векторов, а также пометил бы
квадратный корень вектора как недопустимое
выражение. Но с оператором векторизации и a c как скалярное
произведение векторов, а также пометил бы
квадратный корень вектора как недопустимое
выражение. Но с оператором векторизации и a c, и квадратный
корень вычисляются поэлементно. c, и квадратный
корень вычисляются поэлементно.
Ниже приведены свойства оператора
векторизации:
- Оператор векторизации изменяет значение других
операторов и функций, к которым
применяется. Он не изменяет значений переменных
и чисел. Если применить оператор векторизации к
простой переменной, это просто выведет стрелку
над именем. Можно использовать эту стрелку
только для косметических целей.
- Поскольку операции между двумя массивами
выполняются поэлементно, все массивы под
оператором векторизации должны быть одного
размера. Операции между массивом и скаляром
выполняются применением скаляра к каждому
элементу массива. Например, если v — вектор, а n
— скаляр, применение оператора векторизации к vn
возвращает вектор, чьи элементы есть n-ные
степени элементов v.
- Любую из следующих матричных операций не
удастся использовать под оператором
векторизации: скалярное произведение, умножение
матриц, степени матрицы, обращение матрицы,
вычисление детерминанта, нахождение длины
вектора. Оператор векторизации будет
трансформировать эти операции в поэлементное
перемножение, возведение в степень или
нахождение модуля соответственно.
- Оператор векторизации не влияет на операторы и
функции, требующие в качестве аргумента массив:
транспонирование, векторное произведение,
суммирование элементов вектора, и функции
подобные mean, поскольку они не имеют смысла
для скалярного аргумента.
- Оператор векторизации применяется только к
последнему, скалярному аргументу interp и linterp.
Другие аргументы остаются незатронуты. См. “Интерполяция и функции
предсказания” в Главе “Статистические функции”.
  
|

