  Этот
раздел описывает тригонометрические,
гиперболические и показательные функции Mathcad
вместе с обратными им. Здесь также описываются
встроенные функции Бесселя.
Тригонометрические функции и обратные им.
Тригонометрические функции Mathcad и обратные им
определены для любого комплексного аргумента.
Они также возвращают комплексные значения везде,
где необходимо. Результаты для комплексных
значений вычисляются с использованием тождеств:
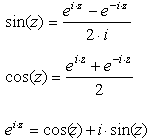
Для применения этих функций к каждому
элементу вектора или матрицы используйте
оператор векторизации.
Обратите внимание, что все эти
тригонометрические функции используют аргумент,
выраженный в радианах. Чтобы перейти к градусам,
используется встроенная единица deg. Например,
чтобы вычислить синус 45 градусов, введите sin(45*deg).
Имейте в виду, что из-за ошибок округления,
свойственных машинной арифметике, Mathcad может
возвращать очень большое число в той точке, где
находится особенность вычисляемой функции.
Вообще, необходимо быть осторожным при
вычислениях в окрестности таких точек.
| sin(z) |
Возвращает синус z. В
прямоугольном треугольнике это — отношение
длины противолежащего катета к длине
гипотенузы. |
| cos(z) |
Возвращает косинус z. В
прямоугольном треугольнике это — отношение
длины прилежащего катета к длине гипотенузы. |
| tan(z) |
Возвращает (sin(z)/cos(z)), тангенс z. В
прямоугольном треугольнике это — отношение
длины противолежащего катета к длине прилежащего
катета; z не должен быть кратным p/2. |
| csc(z) |
Возвращает 1/sin(z), косеканс z; z не
должен быть кратным p. |
| sec(z) |
Возвращает 1/cos(z), секанс z; z не
должен быть кратным p/2. |
| cot(z) |
Возвращает 1/tan(z), котангенс z; z не
должен быть кратным p. |
Из-за ошибок округления, свойственных машинной
арифметике, в результате вычисления atan
достаточно большого числа получается значение .
Как правило, лучше всего избегать численных
вычислений около таких особенностей.
| asin(z) |
Возвращает угол (в радианах), чей
синус — z. |
| acos(z) |
Возвращает угол (в радианах), чей
косинус — z. |
| atan(z) |
Возвращает угол (в радианах), чей
тангенс — z. |
Гиперболические функции sinh и cosh
определяются формулами:
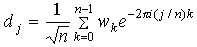
Эти функции также могут использовать
комплексный аргумент и возвращать комплексные
значения. Гиперболические функции тесно связаны
с тригонометрическими функциями. Справедливы
формулы:
sinh(i z)=i z)=i sin(z)cosh(i sin(z)cosh(i z)=cos(z) z)=cos(z)
| sinh (z) |
Возвращает гиперболический
синус z. |
| cosh (z) |
Возвращает гиперболический
косинус z. |
| tanh (z) |
Возвращает sinh(z)/cosh(z),
гиперболический тангенс z. |
| csch (z) |
Возвращает 1/sinh(z),
гиперболический косеканс z. |
| sech (z) |
Возвращает 1/cosh(z),
гиперболический секанс z. |
| coth (z) |
Возвращает 1/tanh(z),
гиперболический котангенс z. |
| asinh (z) |
Возвращает число, чей
гиперболический синус — z. |
| acosh (z) |
Возвращает число, чей
гиперболический косинус — z. |
| atanh (z) |
Возвращает число, чей
гиперболический тангенс — z. |
Логарифмические и показательные функции Mathcad
могут использовать комплексный аргумент и
возвращать комплексные значения. Значения
экспоненциальной функции для комплексного
аргумента вычисляются с применением формулы
ex+iy=ex(cos(y) + i sin(y)) sin(y))
Вообще говоря, значения натурального логарифма
даются формулой
ln(x + i y)=ln|x + i y)=ln|x + i y|+ atan(y/x) y|+ atan(y/x) i + 2 i + 2 n n p p i i
В Mathcad функция ln возвращает значение,
соответствующее n = 0. А именно:
ln(x + i y)=ln|x + i y)=ln|x + i y|+ atan(y/x) y|+ atan(y/x) i i
Оно называется основным значением логарифма.
Рисунок 1 иллюстрирует некоторые основные
свойства логарифма.
| exp(z) |
Возвращает e в степени z. |
| ln(z) |
Возвращает натуральный логарифм
z. (z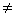 0). 0). |
| log(z) |
Возвращает логарифм z по
основанию 10. (z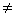 0). 0). |

Рисунок 1: Использование логарифмических
функций.
Функции Бесселя
Эти функции обычно возникают как решения для
волнового уравнения, подчиненного
цилиндрическим граничным условиям.
Функции Бесселя первого и второго рода, Jn(x)
и Yn(x), являются решениями для
дифференциального уравнения
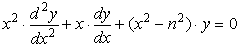
Модифицированные функции Бесселя первого и
второго рода, In(x) и Kn(x), являются
решениями для немного видоизмененного
уравнения:
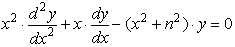
| J0(x) |
Возвращает J0(x); x
вещественный. |
| J1(x) |
Возвращает J1(x); x
вещественный. |
| Jn(m, x) |
Возвращает Jn(x); x
вещественный, 0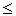 m m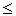 100. 100. |
| Y0(x) |
Возвращает Y0(x); x
вещественный, x > 0. |
| Y1(x) |
Возвращает Y1(x); x
вещественный, x > 0. |
| Yn(m, x) |
Возвращает Yn(x). x > 0, 0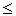 m m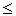 100 100 |
| I0(x) |
Возвращает I0(x); x
вещественный. |
| I1(x) |
Возвращает I1(x); x
вещественный. |
| In(m, x) |
Возвращает In(x); x
вещественный, 0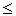 m m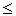 100. 100. |
| K0(x) |
Возвращает K0(x); x
вещественный, x > 0. |
| K1(x) |
Возвращает K1(x); x
вещественный, x > 0. |
| Kn(m, x) |
Возвращает Kn(x). x > 0, 0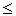 m m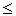 100 100 |
Следующие функции возникают в широком круге
задач.
| erf(x) |
Возвращает значение интеграла
ошибок в x: 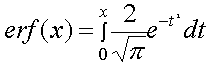
x должен быть вещественным. |
| G(z) |
Возвращает значение эйлеровой
гамма-функции в z. Для вещественного z
значения этой функции совпадают со следующим
интегралом: 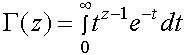
Для комплексных z значения — аналитическое
продолжение вещественной функции. Гамма-функция
Эйлера неопределена для z= 0,-1,-2, ...
Гамма-функция Эйлера удовлетворяет
рекуррентному соотношению
Г(z +1) = zГ(z)
Откуда следует для положительных целых z:
Г(z +1) = z!.
Интеграл ошибок часто возникает в статистике.
Он может также быть использован для определения
дополнения интеграла ошибок по формуле:
erfc(x) := 1 - erf(x) |
  
|

