  Кусочно-непрерывные функции полезны
для управления ветвлениями и остановками
вычислительных процессов. Имеются пять функций
Mathcad, относящихся к этому классу. Функция if полезна
для выбора одного из двух значений,
определяемого условием. Ступенчатая функция
Хэвисайда и символ Кронекера d(m,
n) во многом аналогичны функции if. Кусочно-непрерывные функции полезны
для управления ветвлениями и остановками
вычислительных процессов. Имеются пять функций
Mathcad, относящихся к этому классу. Функция if полезна
для выбора одного из двух значений,
определяемого условием. Ступенчатая функция
Хэвисайда и символ Кронекера d(m,
n) во многом аналогичны функции if.
Функция until используется, чтобы управлять
процессом итераций. Это единственая из функций
Mathcad, специально предназначенная для работы
только с дискретным аргументом, она может
остановить итерации при достижении некоторого
заданного условия.
В Mathcad PLUS можно использовать возможности
программирования для выполнения логических
ветвлений и циклов в вычислениях. См. описание
возможностей программирования Mathcad в Главе "Программирование".
Последняя функция — e,
полностью антисимметричный тензор. Она
возвращает 0, 1 или -1 в зависимости от
перестановки аргументов. Хотя эта функция имеет
ограниченную применимость, было бы трудно
заменить её, используя комбинацию любых других
функций Mathcad.
Функция if
Функция if используется для определения
функции, которая ведет себя по-разному слева и
справа от некоторой точки. Эта точка разрыва
определяется первым аргументом, cond.
Другие два аргумента позволяют определить
поведение функции по обе стороны от точки
разрыва.
| if (cond, tval, fval) |
Возвращает значение tval, если cond
отличен от 0 (истина) Возвращает значение fval, если
cond равен 0 (ложь). |
Хотя аргумент cond может быть любым
выражением, обычно удобнее использовать
какое-либо булево выражение из таблицы,
приведенной ниже. В этой таблице через x и y
обозначены вещественные скаляры, а через w и z
— комплексные скаляры.
| Условие |
Как ввести |
Описание |
| w = z |
[Ctrl]= |
Булево равенство возвращает 1,
если операнды равны; иначе 0 |
| x > y |
> |
Больше чем. |
| x < y |
< |
Меньше чем. |
x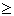 y y |
[Ctrl]0 |
Больше либо равно. |
x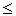 y y |
[Ctrl]9 |
Меньше либо равно. |
w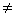 z z |
[Ctrl]3 |
Не равно. |
Обратите внимание, что булевы
выражения, включая неравенства, не могут
использоваться с комплексными числами,
поскольку бессмысленно говорить относительно
одного комплексного числа, что оно является
большим или меньшим, чем другое.
Чтобы сохранить время, Mathcad вычисляет только те
выражения, которые необходимо. Например, если cond
есть ложь, нет нужды вычислять tval, так как его
значение не будет возвращено. Из-за этого ошибки
в невычисляемом выражении могут выпасть из поля
зрения. Например, Mathcad никогда не обнаружит, что в
выражении ниже ln(0) не определён:
if(|x| < 0 , ln(0) , ln(x))
Рисунок 5 показывает некоторые формулы,
использующие функцию if. Вы можете
объединять булевы операторы, чтобы записать
более сложные условия. Например, условие
(x < 1) (x > 0) (x > 0)
действует подобно логическому “и”,
возвращающему 1, только если x заключено между
0 и 1. Аналогично, выражение
(x > 1)+(x < 0)
действует подобно логическому “или”,
возвращающему 1, если или x>1, или x< 0, но не если x
заключено между 0 и 1.
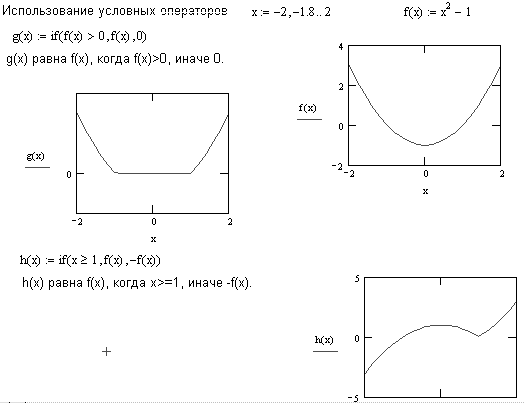
Рисунок 5: Условные выражения в Mathcad.
Функция until
Функция until позволяет останавливать
вычисления, когда выполняется определенное
условие. Её первый аргумент должен включать
дискретную переменную. Mathcad будет выполнять
вычисления для последовательных значений
дискретного аргумента, пока первый аргумент until
не станет отрицательным. Когда это случается,
Mathcad останавливает вычисления.
| until (x, z) |
Возвращает z, пока выражение x
не становится отрицательным; x должно
содержать дискретный аргумент. |
Не используйте функции until в
формулах с несколькими дискретными аргументами
(например, в кратных суммах). Mathcad будет
останавливать все вычисления по всем дискретным
аргументам, как только первый аргумент until
станет отрицателен. Это обычно не дает желаемого
результата.

Рисунок 6: Использование функции until для
остановки вычислений.
Функция until полезна в итерационных
процессах с определенным условием сходимости.
Например, Рисунок 6 показывает, как использовать
функцию until, чтобы проверить итерационный
процесс на сходимость. Вычисления по формуле для
продолжаются, пока не попадет внутрь интервала
полуширины err с центром в точке a. Рисунок 6
также показывает, как использовать функцию last,
чтобы обнаружить, когда вычисления были
остановлены, и вычислить размер возникающего в
результате массива. При использовании функции until
убедитесь, что значение первого аргумента
изменяется где-нибудь в процессе итерации. Иначе
можно оказаться в бесконечном цикле. Если это
случится, нажмите [Esc], чтобы прервать
вычисления.
Импульсные и ступенчатые функции
Эти две функции используют функцию if.
Cтупенчатая функция Хэвисайда эквивалентна
следующей:
F (x) := if(x < 0,0,1)
Для целых m и n символ Кронекера
эквивалентен функции
d (m, n):= if(m = n, 1,0)
| Ф(x) |
Cтупенчатая функция Хэвисайда.
Возвращает 1, если x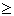 0; иначе 0. 0; иначе 0. |
| d(m, n) |
Символ Кронекера. Возвращает 1,
если m=n; иначе 0. Оба аргумента должны быть
целочисленными. |
pulse(x,w):= Ф(x) - Ф(x-w)
Можно определить также две полезные функции
lowpass и highpass. Они обе являются фильтрами —
умножение на них какого-либо сигнала вырезает из
этого сигнала кусок вокруг точки x, имеющий
ширину 2w. Разница состоит в том, что lowpass оставляет
только вырезанный кусок, highpass — всё, кроме
вырезанного куска.
lowpass(x,w):= pulse(x+w,2*w)
highpass(x,w):= 1 - pulse(x+w,2*w)
Рисунок 7 иллюстрирует использование
ступенчатой функции Хэвисайда для создания
фильтров.

Рисунок 7: Использование ступенчатой функции
Хэвисайда для фильтрации.
e - функция
Аргументы этой функции — три целых числа между
0 и 2 включительно. Она определяет, сколько раз
необходимо сделать перестановку двух
аргументов, чтобы вернуться к
последовательности [0, 1, 2] из той
последовательности [i, j, k], которая передана
ей в качестве аргументов.
Конкретно: e(i, j, k) = 1,
если [i, j, k]— четная перестановка [0, 1, 2], и e(i, j, k) = -1, если [i, j, k]-
нечетная перестановка . Это объясняет, почему e(0, 1, 2) = 1.
Например, e(2, 0, 1) = 1,
поскольку, чтобы перейти из [2, 0, 1] обратно к [0, 1, 2],
требуется дважды менять аргументы местами. С
другой стороны, e(0, 2, 1) = -1,
поскольку чтобы перейти из [0, 2, 1] обратно к [0, 1, 2],
необходимо менять аргументы местами один раз.
Если два аргумента одинаковы, например e(0, 1, 1), нельзя вернуться к [0, 1, 2],
поэтому функция возвращает 0.
Хотя эта функция используется не очень часто,
она незаменима, когда нужно посчитать
перестановки. Очень трудно выполнить эту
замысловатую операцию, используя комбинации
любых других функций Mathcad.
| e
(i, j, k) |
Полностью антисимметричный
тензор ранга 3. i, j и k должны быть целыми
числами между 0 и 2 включительно (или между ORIGIN и
ORIGIN + 2 включительно, если ORIGIN 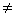 0). Результат 0, если любые два
аргумента одинаковы, 1 для четных перестановок,-1
для нечетных перестановок. 0). Результат 0, если любые два
аргумента одинаковы, 1 для четных перестановок,-1
для нечетных перестановок. |
  
|

