Руководство пользователя Mathcad


Купить Matlab \| Mathematica \| Mathcad \| Maple \| Statistica \| Другие пакеты
Internet-класс \| Примеры \| Методики \| Форум \| Download

Встроенные функции

Вставка встроенных функций

Трансцендентные функции

Усечение и функции округления

Дискретные преобразования

Функции сортировки

Кусочно-непрерывные функции

В начало книги

Список встроенных функций

Дискретные преобразования

Mathcad содержит функции для выполнения быстрого дискретного преобразования Фурье (БПФ) и его обращения. В Mathcad PLUS имеется также одномерное дискретное волновое преобразование и его обращение. Все эти функции имеют векторные аргументы. При определении вектора v для нахождения волнового преобразования или преобразования Фурье убедитесь, что первый элемент вектора имеет нулевой индекс: v₀. Если элемент v₀ не определен, Mathcad автоматически устанавливает его равным 0. Это может привести к искажению результата.

Введение в дискретное преобразование Фурье

В Mathcad входят два типа функций для дискретного преобразования Фурье: fft/ifft и cfft/icfft . Эти функции дискретны: они берут в качестве аргументов и возвращают векторы и матрицы. Они не могут быть использованы с другими функциями.

Используйте функции fft и ifft, если выполнены следующие два условия:

аргументы вещественны, и
вектор данных имеет 2^m элементов.

Используйте функции cfft и icfft во всех других случаях.
Первое условие необходимо, потому что функции fft/ifft используют тот факт, что для вещественных данных вторая половина преобразования Фурье является комплексно сопряженной с первой. Mathcad отбрасывает вторую половину вектора-результата. Это сохраняет и время и память при вычислениях.

Пара функций cfft/icfft не использует симметрию в преобразовании. По этой причине необходимо использовать их для комплексных данных. Так как вещественные числа — подмножество комплексных чисел, можно также использовать пару cfft/icfft для вещественных чисел.

Второе условие требуется, потому что пара функций fft/ifft использует высоко эффективный алгоритм быстрого преобразования Фурье. Для этого вектор аргумента, используемого с fft, должен иметь 2^m элементов. В функциях сfft/icfft использован алгоритм, который допускает в качестве аргументов как матрицы, так и векторы произвольного размера. Когда эта пара функций используется с матрицей в качестве аргумента, вычисляется двумерное преобразование Фурье.

Обратите внимание, что, если использована функция fft для прямого преобразования, необходимо использовать функцию ifft для обратного. Аналогично, если для прямого преобразования использована cfft, то для обратного необходимо использовать icfft.

Различные формулировки определения преобразования Фурье используют различные нормировочные коэффициенты и соглашения о знаке перед мнимой единицей в показателе экспоненты прямого и обратного преобразований. Функции fft, ifft, cfft и icfft используют 1/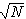 как нормировочный коэффициент и положительный показатель степени в прямом преобразовании. Функции FFT, IFFT, CFFT и ICFFT используют 1/N как нормировочный коэффициент и отрицательный показатель степени в прямом преобразовании. Необходимо использовать эти функции попарно. Например, если используется CFFT в прямом преобразовании, необходимо использовать ICFFT в обратном.

Преобразование Фурье в вещественной области

Для вещественнозначных векторов с 2^m элементами можно применять пару функций fft/ifft. В алгоритме вычисления этих функций используются преимущества симметрии, существующей только для вещественных данных. Это позволяет сохранить и время, и память, необходимые для вычислений.

fft (v)

Возвращает дискретное преобразование Фурье 2^m-мерного вещественнозначного вектора. Аргумент можно интерпретировать как результат измерений через равные промежутки времени некоторого сигнала.

Вектор v должен иметь 2^m элементов. Результат — комплекснозначный вектор размерности 1+2^m-1. Если v имеет размерность отличную от 2^m, Mathcad выдает сообщение об ошибке “неверный размер вектора”.

Элементы вектора, возвращаемого fft, вычисляются по формуле

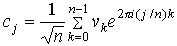
В этой формуле n — число элементов в v, i — мнимая единица.

Элементы в векторе, возвращенном функцией fft, соответствуют различным частотам. Чтобы восстанавливать фактическую частоту, необходимо знать частоту измерения исходного сигнала. Если v есть n-мерный вектор, переданный функции fft, и частота измерения исходного сигнала — f_s, то частота, соответствующая , равна

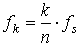
Обратите внимание, что это делает невозможным обнаружить частоты выше частоты измерения исходного сигнала. Это — ограничение налагаемое не Mathcad, а самой сутью проблемы. Чтобы правильно восстанавливать сигнал по его преобразованию Фурье, необходимо произвести измерения исходного сигнала с частотой, по крайней мере вдвое большей, чем ширина полосы частот. Полное обсуждение этого явления лежит за пределами данного руководства, но его можно найти в любом учебнике по цифровой обработке сигналов.

ifft (v)

Возвращает обратное дискретное преобразование Фурье; результат — вещественнозначный.

Вектор v должен иметь 1+ 2^m элементов, где m — целое. Результат есть комплекснозначный вектор размерности 2^m+1. Если v имеет размерность, отличную от 1+ 2^m, Mathcad выдает сообщение об ошибке “неверный размер вектора”.

Аргумент v — вектор, подобный созданному функцией fft. Чтобы вычислить результат, Mathcad сначала создает новый вектор w, комплексно сопряженный v, и присоединяет его к вектору v. Затем Mathcad вычисляет вектор d, чьи элементы вычисляются по формуле:

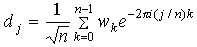
Это та же самая формула, что и для fft, кроме знака минус в функции exp. Функции fft и ifft — точные обращения. Для всх вещественнозначных v справедливо ifft(fft(v))=v.

Преобразование Фурье в комплексной области

Имеются две причины, по которым не могут быть использованы пары преобразований fft/ifft, обсужденные в предыдущем разделе:

Данные могут быть комплекснозначны. Это означает, что Mathcad не может больше использовать симметрию, имеющую место в вещественном случае.
Вектор данных может иметь размерность, отличную от 2^m. Это означает, что Mathcad не может пользоваться преимуществом высокоэффективного алгоритма БПФ, используемого парой fft/ifft.

Комплексное преобразование Фурье требует следующих функций:

cfft (A)	Возвращает дискретное преобразование Фурье комплекснозначных вектора или матрицы. Возвращаемый массив имеет тот же самый размер, что и массив, используемый как аргумент.
icfft (A)	Возвращается обращение дискретного преобразования Фурье вектора или матрицы данных. Функция icfft — обратная к функции cfft. Подобно cfft, эта функция возвращает массив того же самого размера, что и аргумент.

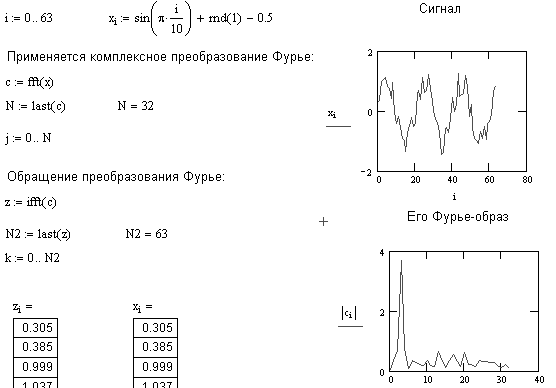3_280.gif (6502 bytes)

Рисунок 3: Использование быстрых преобразований Фурье в Mathcad.

Пара преобразований cfft/icfft может работать с массивами любого размера. Однако они работают значительно быстрее, когда число строк и столбцов может быть представлено в виде произведения большого количества меньших сомножителей. Например, векторы с длиной 2^m относятся к этому классу, так же как и векторы, имеющие длины, подобные 100 или 120. С другой стороны, вектор, чья длина — большое простое число, замедлит вычисление преобразования Фурье.

Функции cfft и icfft — обратные друг к другу. То есть icfft(cfft(v))=v. Рисунок 3 показывает примеры использования преобразования Фурье в Mathcad.

Когда в качестве аргумента cfft используется матрица, результат есть двумерное преобразование Фурье исходной матрицы.

Альтернативные формы преобразования Фурье

Определения преобразования Фурье, обсужденные выше, не являются единственно возможными. Например, следующие определения для дискретного преобразования Фурье и его обращения можно найти в книге Ronald Bracewells, The Fourier Transform and Its Applications (McGraw-Hill, 1986):

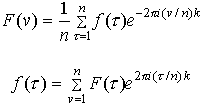f14.gif (1733 bytes)

Эти определения весьма распространены в технической литературе. Чтобы использовать эти определения вместо обсужденных в предыдущем разделе, используйте функции FFT, IFFT, CFFT и ICFFT. Они отличаются следующим:

Вместо коэффициента 1/ 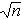перед обеими формулами в прямом преобразовании стоит коэффициент 1/n, и коэффициент 1 в обратном преобразовании.
Знак минус появляется в показателе экспоненты прямого преобразования и исчезает в формуле обратного.

Функции FFT, IFFT, CFFT и ICFFT используются аналогично функциям, обсужденным в предыдущем разделе.

Волновое преобразование

A Mathcad PLUS включены две функции волновых преобразований: для выполнения прямого одномерного дискретного волнового преобразования и его обращения. Преобразование выполняется с использованием четырехкоэффициентного волнового базиса Даубечи.

Е wave (v)	Возвращает дискретное волновое преобразование v, 2^m-мерного вещественнозначного вектора. Возвращается вектор того же самого размера, что и v.
Е iwave (v)	Возвращает обращение дискретного волнового преобразования v, 2^m-мерного вещественнозначного вектора. Возвращается вектор того же самого размера, что и v.

Список встроенных функций

| На первую страницу | Поиск | Купить Matlab

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Дата последнего обновления информации на сайте: 04.03.17
Сайт начал работу 01.09.00