Пример 1 ~ Пример 2 ~ Пример 3

Пример 1. Значение производной функции комплексного переменного в точке.
Дана функция  f(z) = z³. Вычислим значение  f ' (z) в точке z₀=1+i, ее модуль и аргумент.
Поскольку
(z³)' =3z², то
f '(z₀) = 3z₀²;   |f '(z₀)| = 3| z₀|²;   arg f ' (z₀) = 2arg z₀,
имеем:

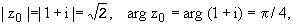
то
f ' (1+ i) = 3(1+ i)² = 6i, |f ' (1+ i)| = 6, arg f ' (1+ i) = p/2.
Иначе:

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

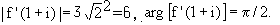
Пример 2. Исследование дифференцируемости функции.

Дана функция f(z) = |z|².
Находим   u(x, y) = Re f(z) = x² + y²,  v(x, y) =Im f(z)=0.
Определяем частные производные:

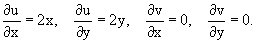
Условия Коши-Римана выполняются только при x = y = 0, т.е. в точке
z = 0. Непрерывность частной производной очевидна. Следовательно, функция f(z) = |z|² дифференцируема только в нуле (в точке z = 0).

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 3. Исследование дифференцируемости функции, вычисление производной.

Дана функция f(z) = e^z.
Из равенства e^z = e^x (cosy + isiny) находим
u(x, y) = e^x cosy,  v(x, y) = e^x siny.
Находим частные производные:

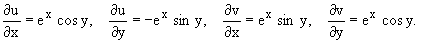
Условия Коши-Римана выполняются в любой точке z, принадлежащей комплесной области, и частные производные непрерывны повсюду. Следовательно, функция e^z дифференцируема всюду в комлексной области.
Используя найденные частные производные, записываем производную функции:

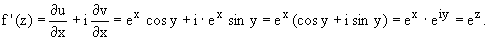
Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica