Производная функции комплексного переменного ~ Правила дифференцирования ~ Дифференцирование сложной функции ~ Условия Коши-Римана

Производная функции комплексного переменного определяется, как и производная в действительной области:

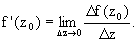
Здесь
z₀, Dz ^_  комплексные и Df(z₀) = f(z₀+Dz) - f(z).

Используя это определение и свойства пределов, несложно убедиться в справедливости следующих правил дифференцирования.

1. Сумма и произведение дифференцируемых в точке функций,  есть функция и справедливы равенства:

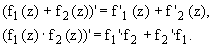
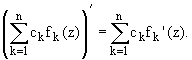
2. Частное дифференцируемых в точке функций, при условии, что знаменатель в точке не равен нулю, есть дифференцируемая в этой точке функция, :

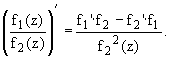
3. Сложная функция f(j (z)) дифференцируема в точке z₀, если в этой точке дифференцируема функция j (z), а функция f(u) дифференцируема в точке u₀,
где u₀ = j (z₀) и u = j (z). При этом в точке z₀ имеет место формула:

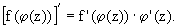
Для элементарных функций комплексного переменного справедливы формулы дифференцирования, установленные для действительных значений аргумента.
Например, рассмотрим функцию  f(z) = z³.
По определению производной для любой точки z, принадлежащей комплексной области, записываем:

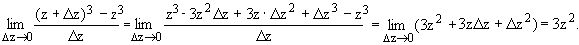
Предел существует для любой точки z, принадлежащей комплексной области и
(z³)' =3z².
Аналогично можно получить:
(zⁿ)' = nzⁿ-1 (n - действительное число).

ПРИМЕР 1. Вычисление значения производной функции коплексного переменного в точке.

Если f(z) = f(x+iy) = u(x, y) + iv(x, y), т.е. u(x, y) = Re f(z) и v(x, y) = Im f(z),
то справедливы следующие утверждения:

1. Если функция f(z) дифференцируема в точке, то в этой точке существуют частные производные ее действительной и мнимой частей
u(x, y) = Re f(z),   v(x, y) = Im f(z)
и выполняется условие Коши-Римана:

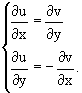
2. Если u(x, y)  и v(x, y) дифференцируемы в точке (x₀, y₀) (имеют непрерывные частные производные в этой точке) и выполняется условие Коши-Римана, то функция   f(z) = f(x+iy) = u(x, y) + iv(x, y)  дифференцируема в точке z₀ = x₀+ iy₀.

3. Производная дифференцируемой функции может быть записана по одной из формул:

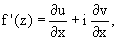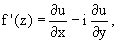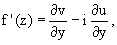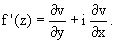
ПРИМЕР 2. Исследование дифференцируемости функции.

ПРИМЕР 3. Исследование дифференцируемости функции, вычисление производной.