Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример 4 ~ Пример 5 ~ Пример 6

Пример 1.    Различные формы записи дифференциальных уравнений первого порядка.

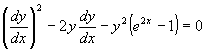
xdy + (y - cosx)dx = 0

y' + 2y = e^x 

Те же уравнения, записанные в нормальной форме.

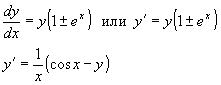
y' = e^x - 2y 

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 2. Проверка правильности решения дифференциального уравнения первого порядка.

Покажем, что 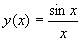  решение уравнения  xdy + (y - cosx)dx = 0.
Для этого вычислим dy и подставим его в уравнение: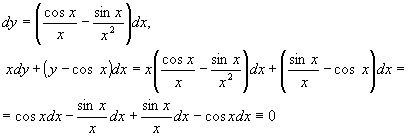

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 3. Интегральные кривые и графики решений дифференциальных уравнений.

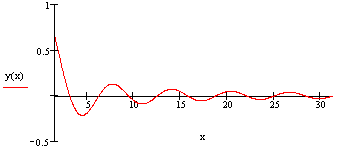
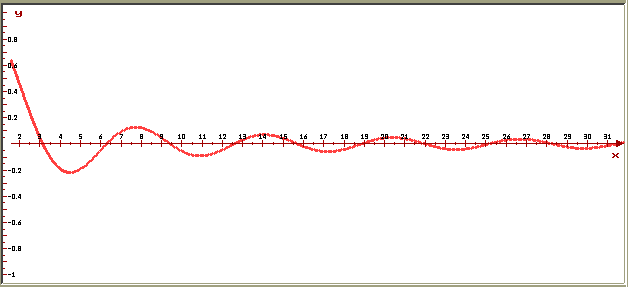
На рисунках изображена интегральная кривая — график решения дифференциального уравнения xdy + (y - cosx)dx, проходящего через точку с координатами (p/2, 2/p), построенная в Mathcad и в ОДУ.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 4. Поле направлений и интегральные кривые

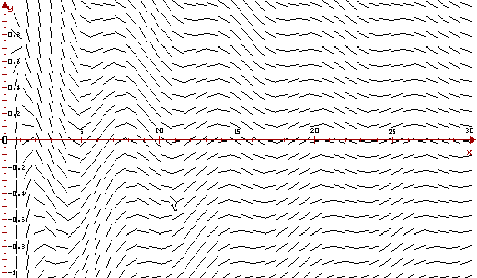
На рисунке изображено поле направлений дифференциального уравнения      xdy + (y - cosx)dx,   построенное в ОДУ.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 5. Общее решение дифференциального уравнения

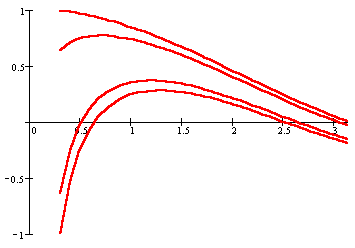
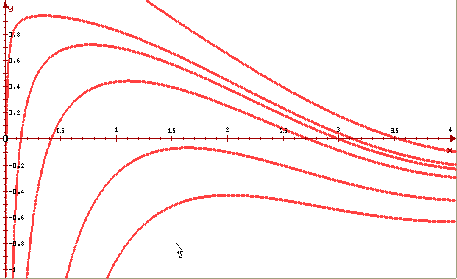
На рисунках изображены несколько интегральных кривых   дифференциального уравнения xdy + (y - cosx)dx, построенных в Mathcad и в ОДУ.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 6. Пример нарушения единственности решения задачи Коши

Рассмотрим уравнение

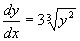
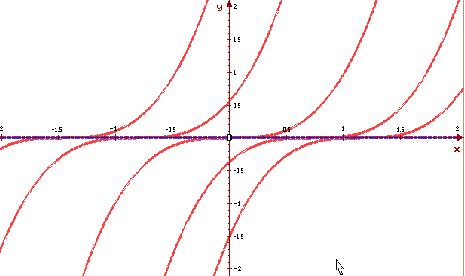
Его правая часть непрерывна всюду, а частная производная правой части при y=0 не существует. На рисунке, построенном в  ОДУ видно, что через каждую точку с координатами
x= C , y = 0 проходит два решения: y=0 и y = (x - C)³.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica