Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример 4

Пример 1. Изобразим график решения и фазовую траекторию уравнения Вольтерра-Лотка

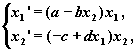
для a=4, b=2.5, c=2, d=1 и графики ее решения с начальным условием x₁(0)=3, x₂(0)=1.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 2.  Изобразим график решения и фазовую траекторию модели конкурирующих видов с “логистической поправкой”:

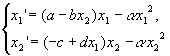
для  a =0.1, a=4, b=2.5, c=2, d=1  с начальным условием x₁(0)=3, x₂(0)=1.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 3. Изобразим график решения и фазовую траекторию модели конкурирующих видов  Холлинга—Тэннера:

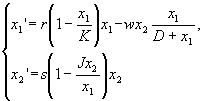
при r =1, K=7, w=1.5, D=1, s=0.2, J=0.5 и начальном состоянии:
x=3, y=1 и x=1, y=1.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 4. Изобразим график решения и фазовую траекторию модели   выравнивания цен по уровню актива имеет вид
q' = k(s(p) - d(p)),
p' = - m(q-q₀)
для s(p)=ap+s₀ , d(p)=cp+d₀ , k=0.3, m=0.1, q₀ =20, a=20, s₀ =10, d₀ =50, c=-10 при начальном состоянии q(0)=3, p(0)=1.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica