Динамика
популяций ~ Уравнения
Вольтерра-Лотка ~ Уравнения
Вольтерра-Лотка с логистической поправкой ~ Модель Холлинга-Тэннера ~ Выравнивание цен
Дифференциальные уравнения широко
используются для моделирования реальных систем,
зависящих от времени, в частности, для описания и
исследования экономических и биологических
систем.
Динамика популяций. Уравнения
Вольтерра-Лотка
В динамике популяций есть много примеров, когда
изменение численности популяций во времени
носит колебательный характер. Одним из самых
известных примеров описания динамики
взаимодействующих популяций являются уравнения
Вольтерра—Лотка. Рассмотрим модель
взаимодействия хищников и их добычи, когда между
особями одного вида нет соперничества.
Пусть x1 и x2 — число жертв и
хищников соответственно. Предположим, что
относительный прирост жертв x1'/x1
равен a-bx2, a>0, b>0, где a
— скорость размножения жертв в отсутствие
хищников, -bx2 — потери от хищников.
Развитие популяции хищников зависит от
количества пищи (жертв), при отсутствии пищи ( x1=0
) относительная скорость изменения популяции
хищников равна 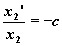 , c>0 , наличие пищи компенсирует
убывание, и при x1>0 имеем , c>0 , наличие пищи компенсирует
убывание, и при x1>0 имеем 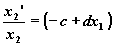 , d>0. , d>0.
Таким образом, система Вольтерра—Лотка имеет
вид:
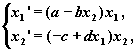
где a, b, c, d >0.
Рассмотренная модель может описывать поведение
конкурирующих фирм, рост народонаселения,
численность воюющих армий, изменение
экологической обстановки, развитие науки и пр.
Рассмотрим фазовый портрет
системы Вольтерра—Лотка для a=4, b=2.5, c=2,
d=1 и графики ее решения с начальным условием x1(0)=3,
x2(0)=1, построенные программой ОДУ.

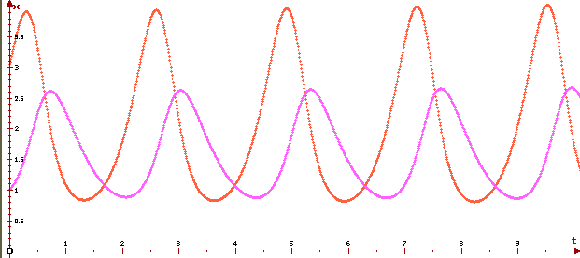
Видно, что процесс имеет колебательный
характер. При заданном начальном соотношении
числа особей обоих видов 3 : 1 , обе популяции
сначала растут. Когда число хищников достигает
величины b=2.5 , популяция жертв не успевает
восстанавливаться и число жертв начинает
убывать. Уменьшение количества пищи через
некоторое время начинает сказываться на
популяции хищников и когда число жертв достигает
величины x1=c/d =2 (в этой точке x2'=0),
число хищников тоже начинает сокращаться вместе
с сокращением числа жертв. Сокращение популяций
происходит до тех пор, пока число хищников не
достигнет величины x2=a/b =1.6 (в этой
точке x1'=0).С этого момента начинает
расти популяция жертв, через некоторое время
пищи становится достаточно, чтобы обеспечить
прирост хищников, обе популяции растут, и ...
процесс повторяется снова и снова. На графике
четко виден периодический характер процесса.
Количество жертв и хищников колеблется возле
величин x1=2, x2=1.6
соответственно (дробные числа здесь не означают
“половину волка”, величины могут измеряться в
сотнях, тысячах и т.п.). Периодичность процесса
явственно видна на фазовой
плоскости — фазовая кривая
(x1(t), x2(t)) —
замкнутая линия. Самая левая точка, этой кривой, -
это точка, в которой число жертв достигает
наименьшего значения. Самая правая точка x1=4,
x2=1.6 , — точка пика популяции жертв.
Между этими точками количество хищников сначала
убывает, до нижней точки фазовой кривой,x1=2
, где достигает наименьшего значения, а затем
растет до верхней точки фазовой кривой (x1=2,
x2=2.5). Фазовая кривая охватывает точку x1=2,
x2=1.6.
На языке дифференциальных уравнений это
означает, что система имеет стационарное
состояние
x1' =0, x2' =0,
которое достигается в точке x1=2, x2=1.6.
Если в начальный момент система находилась в стационарной точке, то
решения x1(t), x2(t) не
будут изменяться во времени, останутся
постоянными. Всякое же другое начальное
состояние приводит к периодическому колебанию
решений. Неэллиптичность формы траектории,
охватывающей центр, отражает негармонический
характер колебаний.
Рассмотренная модель может описывать
поведение конкурирующих фирм, рост
народонаселения, численность воюющих армий,
изменение экологической обстановки, развитие
науки и т.п.
ПРИМЕР 1 . Динамика популяций.
Уравнения Вольтерра-Лотка с
логистической поправкой
Рассмотрим модель конкурирующих видов с
“логистической поправкой”:
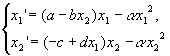
В этом случае поведение решений в окрестности стационарной точки меняется в
зависимости от величины и знака параметра a.
Рассмотрим фазовый портрет
системы Вольтерра—Лотка для a =0.1, a=4,
b=2.5, c=2, d=1 и графики ее решения с
начальным условием x1(0)=3, x2(0)=1,
построенные программой ОДУ.
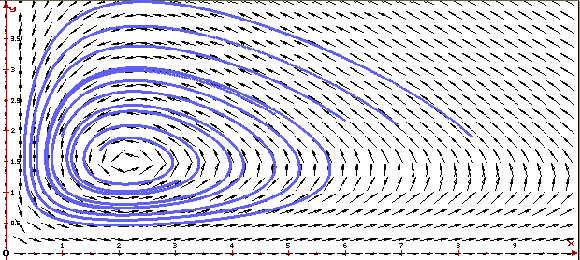
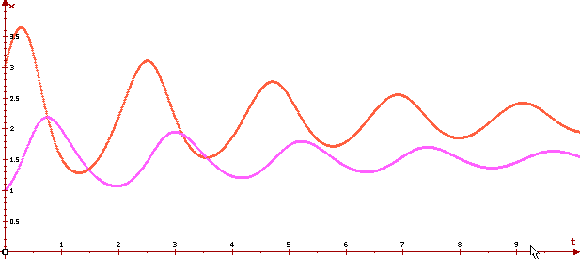
Видно, что в этом случае стационарная точка
превращается в устойчивый
фокус, а решения — в затухающие колебания. При
любом начальном условии состояние системы через
некоторое время становится близким к
стационарному и стремится к нему при 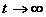 . .
Графики решений и фазовая
кривая при отрицательном значении параметра a,
a =-0.1, приведены ниже.

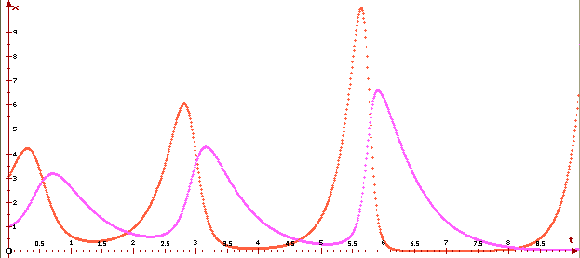
Как видно, в этом случае стационарная
точка является неустойчивым фокусом и
амплитуда колебаний численности видов растет. В
этом случае как бы близко ни было начальное
состояние к стационарному, с течением времени
состояние системы будет сильно отличаться от
стационарного.
ПРИМЕР 2 . Модель
"хищник-жертва" с логистической поправкой.
Модель Холлинга-Тэннера
На примере модели Вольтерра—Лотка и модели
Вольтерра—Лотка с логистической поправкой было
продемонстрировано одно из важнейших
качественных свойств центров
— они легко разрушаются даже при самых малых
изменениях правой части. Большинство моделей
является идеализацией действительности; в них
внимание сосредоточено на некоторых основных
переменных и соотношениях между ними. Поэтому
устойчивость моделей относительно малых
возмущений чрезвычайно важна в приложениях.
Модели, не чувствительные к малым возмущениям,
называются грубыми.
Модель Вольтерра—Лотка неустойчива
относительно возмущений, поскольку ее
стационарное состояние — центр.
Существует другой вид моделей, в которых
возникают незатухающие колебания, — это модели,
имеющие на фазовых портретах предельные
циклы. Такая модель существует для системы
конкурирующих видов — это модель
Холлинга—Тэннера.
Скорость роста популяции жертв x'1 в
этой модели равна сумме трех величин:
- скорости размножения в отсутствие хищников — r
x1;
- влиянию межвидовой конкуренции за пищу при
ограниченных ресурсах (для случая конкурирующих
производителей это влияние ограниченных
сырьевых ресурсов) —
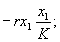
- влиянию хищников , в предположении, что хищник
перестает убивать, когда насыщается —
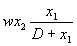
Скорость роста популяции хищников x'2
строится так же, как в модели Вольтерра—Лотка, в
предположении, что жертвы встречаются редко.
Если для поддержания жизни одного хищника нужно J
жертв, то популяция из x1 жертв сможет
обеспечить пищей x1/J хищников.
Модель роста популяции хищников, в которой их
число не может превысить эту критическую
величину, имеет вид
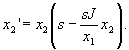 . .
Таким образом, имеем модель Холлинга—Тэннера:
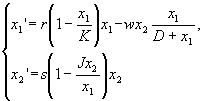
где r, s, K, D, J > 0.
Можно показать, что при
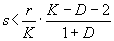
на фазовом портрете
системы будет устойчивый
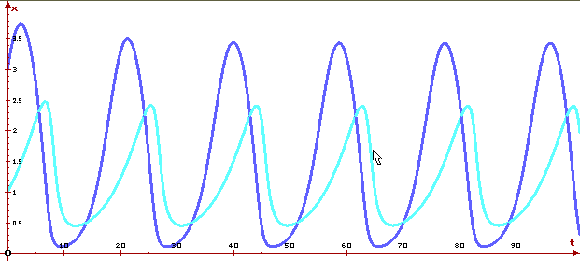
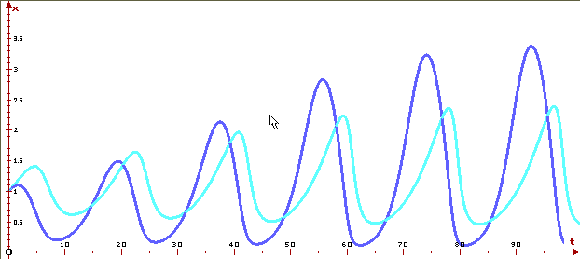
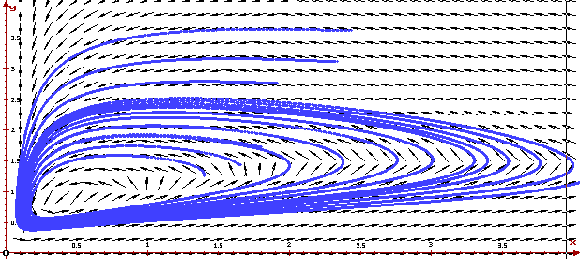
предельный цикл. Ниже приведено решение
системы при r=1, K=7, w=1, D=1, s=0.2,
J=0.5 и двух различных начальных состояниях и
фазовый портрет системы, построенные программой
ОДУ.
ПРИМЕР 3 . Модель
Холлинга-Тэннера.
Выравнивание цен
Модель выравнивания цен по уровню актива
интересна тем, что в ней можно наблюдать
гармонические колебания решений возле стационарного состояния.
Предположим, что изменение уровня актива q пропорционально
разности между предложением s и спросом d,
т.е. q'=k(s-d), k > 0.
Предположим далее, что изменение цены p
пропорционально отклонению актива q от
некоторого фиксированного уровня q0
так, что p'=-m(q-q0 ) , m
> 0. Таким образом, модель выравнивания цен по
уровню актива имеет вид
q' = k(s(p) - d(p)),
p' = - m(q-q0).
Ниже приведены график решения и фазовая кривая для
s(p)=ap+s0 ,
d(p)=cp+d0 ,
k=0.3, m=0.1,
q0 =20, a=20,
s0 =10, d0 =50, c=-10
при начальном состоянии
q(0)=19, p(0)=2,
построенной программой ОДУ.
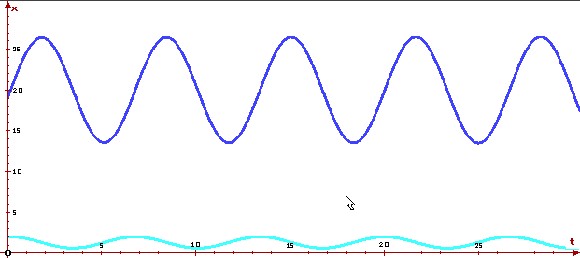
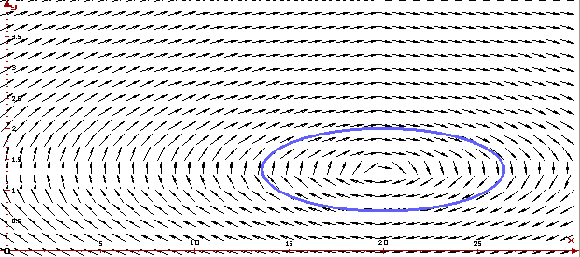
Видно, что цена и актив колеблются возле стационарного состояния. Фазовая траектория
представляет собой эллипс, охватывающий стационарную точку. Это
означает, что колебания актива и цены —
гармонические.
ПРИМЕР 4. Выравнивание цен.

|

