Автономная
система ~ Фазовая кривая ~ Фазовая траектория ~ Фазовый
портрет ~ Фазовая плоскость ~
Фазовое пространство ~ Свойства фазовых траекторий ~ Точка покоя Векторное
поле ~ Векторное поле автономной
системы ~ Особая точка векторного
поля
Система обыкновенных дифференциальных
уравнений называется автономной, если
независимая переменная не входит явно в систему.
В теории автономных систем принято обозначать
независимую переменную буквой t, а искомое
решение — 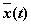 . .
Ограничимся случаем n = 2 и в дальнейшем
рассматриваем автономные системы второго
порядка:
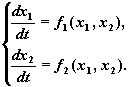
Будем полагать, что правые части системы f1(x1,
x2 ) , f2(x1, x2)
непрерывно дифференцируемы в области 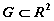 ,
т.е. справедлива теорема
существования и единственности. Название
автономная система оправдано тем, что решение
само управляет своим изменением, поскольку
производные dx1/dt и dx2/dt
зависят только от x1 и x2.
Автономные системы называют также динамическими
системами. ,
т.е. справедлива теорема
существования и единственности. Название
автономная система оправдано тем, что решение
само управляет своим изменением, поскольку
производные dx1/dt и dx2/dt
зависят только от x1 и x2.
Автономные системы называют также динамическими
системами.
Пусть x1=j1(t), x2=
j2(t) — решение автономной системы
второго порядка. Тогда уравнения
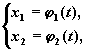
задают в параметрической
форме кривую на плоскости. Эта кривая
называется фазовой кривой или фазовой
траекторией системы. Плоскость, на которой
расположены фазовые траектории называется фазовой плоскостью автономной
системы. Для n >2 фазовые траектории
располагаются в фазовом пространстве.
Если на рисунке изображено несколько фазовых
кривых системы, характеризующих качественное
поведение решений системы (кривые с одинаковыми
асимптотами, предельными точками и пр.), то такое
изображение называется фазовым
портретом системы.
Интегральные кривые рассматриваемой системы
изображаются в трехмерном пространстве
переменных (t, x1, x2) и,
если x1=f1(t),
x2= f2(t) —
решение системы, то интегральная кривая задается
в параметрической форме уравнениями
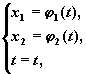
а фазовая траектория — не что иное, как проекция
интегральной кривой на фазовую плоскость
(плоскость (x1, x2).
ПРИМЕР 1 . Фазовые кривые
автономной системы.
Для фазовых кривых (фазовых траекторий)
автономной системы с непрерывно
дифференцируемой правой частью
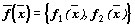 , , 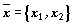 , ,
справедливы следующие утверждения:
- Если существует такая точка
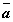 , что , что 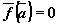 ,
то ,
то 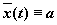 , является решением автономной системы,
т.е. соответствующая фазовая траектория — точка. , является решением автономной системы,
т.е. соответствующая фазовая траектория — точка.
- Если точка (x1(t), x2(t))
принадлежит некоторой фазовой кривой, то при
любой постоянной С точка (x1(t+С),
x2(t+С)) принадлежит той же
фазовой кривой.
- Две фазовые кривые либо не имеют общих точек,
либо совпадают.
- Фазовая траектория, отличная от точки, есть гладкая кривая (в каждой ее
точке есть ненулевой касательный вектор).
- Всякая фазовая кривая принадлежит к одному из
трех типов— гладкая кривая без самопересечений,
замкнутая гладкая кривая (цикл), точка.
- Если фазовая кривая, отвечающая решению
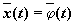 ,
есть гладкая замкнутая кривая, то это решение —
периодическая функция. ,
есть гладкая замкнутая кривая, то это решение —
периодическая функция.
ПРИМЕР 2. Типы фазовых кривых.
Точка 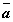 , в которой правая часть
системы обращается в нуль, , в которой правая часть
системы обращается в нуль,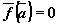 , называется
положением равновесия системы. Положение
равновесия называют также точкой покоя
автономной системы. , называется
положением равновесия системы. Положение
равновесия называют также точкой покоя
автономной системы.
ПРИМЕР 3 . Точки покоя
автономной системы.
Если в каждой точке области 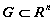 задан n-мерный
вектор задан n-мерный
вектор
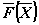 , ,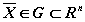 , то говорят, что в области G задано
векторное поле. Запишем автономную
систему второго порядка , то говорят, что в области G задано
векторное поле. Запишем автономную
систему второго порядка
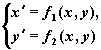
в векторной форме:
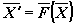
где
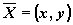 , , 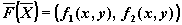
Автономная система
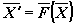
полностью определяется заданием
векторного поля
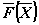 . .
Действительно, в каждой точке
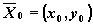
гладкой фазовой кривой
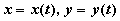
существует касательный вектор
(x'(t0 ), y'(t0 ))
равный (в силу системы) вектору
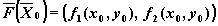 , ,
иными словами, векторное поле
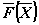
автономной системы задает в каждой точке
направление касательной к фазовой кривой
системы, проходящей через эту точку.
Точки векторного поля, в которых вектор 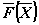 — нулевой, называют особыми
точками векторного поля. Таким образом,
точки покоя автономной системы — это особые
точки векторного поля. — нулевой, называют особыми
точками векторного поля. Таким образом,
точки покоя автономной системы — это особые
точки векторного поля.
ПРИМЕР 4 . Векторное поле
автономной системы.

|

