Кривые на
плоскости в декартовых координатах ~ Кривые, заданные параметрически ~ Кривые в полярных координатах
Кривые на плоскости в декартовых
координатах.
Кривая на плоскости в прямоугольных
(декартовых) координатах — это множество точек,
координаты которых 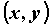 связаны соотношениями связаны соотношениями
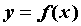 , , 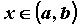 , , 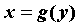 , , 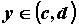 или или 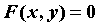 ; первые
два соотношения задают кривую явно, последнее —
неявно. Кривая, заданная уравнением ; первые
два соотношения задают кривую явно, последнее —
неявно. Кривая, заданная уравнением 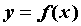 , , 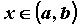 ,
называется гладкой, если функция ,
называется гладкой, если функция 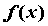 дифференцируема на
промежутке дифференцируема на
промежутке 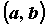 . В каждой точке . В каждой точке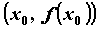 гладкой кривой можно
провести касательную ,
уравнение которой гладкой кривой можно
провести касательную ,
уравнение которой 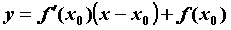 . Уравнение нормали в той же точке имеет
вид . Уравнение нормали в той же точке имеет
вид 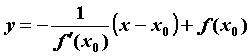 или
или 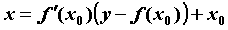 .
Кривая, заданная неявно уравнением .
Кривая, заданная неявно уравнением 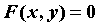 ,
называется гладкой, если на ней нет особых точек (точка ,
называется гладкой, если на ней нет особых точек (точка
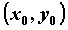 линии линии
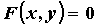 называется
особой, если в ней одновременно обращаются в нуль
обе частные производные функции называется
особой, если в ней одновременно обращаются в нуль
обе частные производные функции 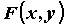 : : 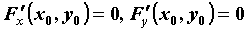 ). Уравнения
касательной и нормали к такой кривой, проходящих
через точку ). Уравнения
касательной и нормали к такой кривой, проходящих
через точку 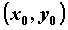 , , 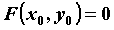 , имеют соответственно вид , имеют соответственно вид 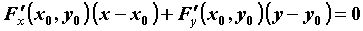 и и 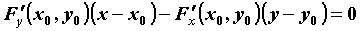
ПРИМЕР 1 . Построение кривой в
декартовых координатах.
Кривые, заданные параметрически.
Уравнения 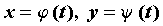 , , 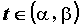 , устанавливающие зависимость
декартовых координат , устанавливающие зависимость
декартовых координат 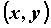 точки плоскости от
значения параметра точки плоскости от
значения параметра 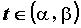 , определяют на
плоскости кривую, заданную в параметрической
форме (говорят еще — заданную параметрически).
Поскольку производная
функции , определяют на
плоскости кривую, заданную в параметрической
форме (говорят еще — заданную параметрически).
Поскольку производная
функции 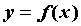 , заданной параметрически уравнениями , заданной параметрически уравнениями 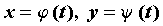 , в
точке, которая не является особой точкой кривой,
вычисляется по формуле , в
точке, которая не является особой точкой кривой,
вычисляется по формуле 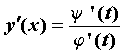 , то уравнения
касательной и нормали к кривой, проходящих через
точку , то уравнения
касательной и нормали к кривой, проходящих через
точку 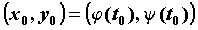 , имеют соответственно вид: , имеют соответственно вид: 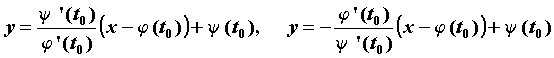 . .
ПРИМЕР 2 . Построение кривой,
заданной параметрически.
Кривые в полярных координатах.
Декартовы координаты точки 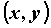 на плоскости связаны
с полярными координатами на плоскости связаны
с полярными координатами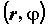 соотношениями соотношениями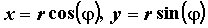 .
Многие кривые на плоскости удобно описывать как
функции радиуса-вектора и полярного угла — в
полярных координатах. Так, уравнение единичной
окружности в полярных координатах имеет вид .
Многие кривые на плоскости удобно описывать как
функции радиуса-вектора и полярного угла — в
полярных координатах. Так, уравнение единичной
окружности в полярных координатах имеет вид 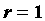 .
Уравнение кривой в полярных координатах
обычно имеет вид .
Уравнение кривой в полярных координатах
обычно имеет вид 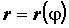 . Угловой коэффициент
касательной к графику функции, заданной
уравнением . Угловой коэффициент
касательной к графику функции, заданной
уравнением 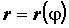 , в точке , в точке 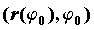 равен равен 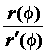 , а
декартовы координаты точки , а
декартовы координаты точки 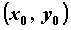 равны соответственно равны соответственно 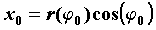 и и 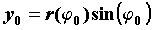 . .
ПРИМЕР 3 . Построение кривой
в полярных координатах.

|

