Производная
функции в точке ~ Односторонние
производные ~ Секущая графика
функции
Касательная и нормаль к графику
функции
Производная функции в точке - Пусть
функция 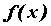 определена на промежутке определена на промежутке 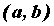 . Точка . Точка 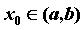 — произвольная точка из
области определения функции, — произвольная точка из
области определения функции, 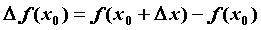 — приращение функции в
точке — приращение функции в
точке 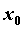 , вызванное приращением , вызванное приращением 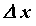 независимой переменной независимой переменной 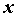 . Производной
функции . Производной
функции 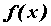 по независимой переменной по независимой переменной 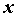 в точке в точке 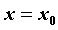 , , 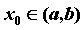 называется
предел отношения
приращения функции называется
предел отношения
приращения функции 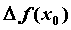 к
приращению к
приращению 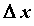 при стремлении при стремлении 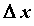 к нулю, т.е. к нулю, т.е.
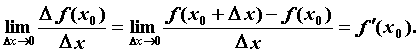
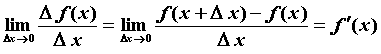 , ,
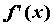 — производная функции в
точке — производная функции в
точке 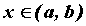 . .
ПРИМЕР 1 . Вычисление
производных
Односторонние производные - Если 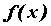 определена при определена при 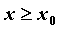 , то можно
определить правую производную функции , то можно
определить правую производную функции 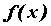 в точке в точке 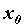 : :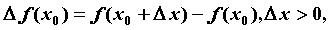 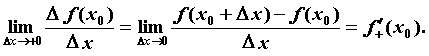
Аналогично, если 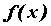 определена при
определена при 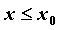 , определяется левая
производная функции в точке , определяется левая
производная функции в точке 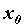 : :
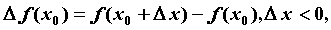
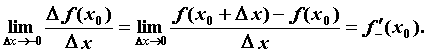
Функция 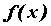 имеет в
точке имеет в
точке 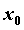 производную производную 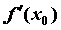 тогда и
только тогда, когда в точке тогда и
только тогда, когда в точке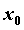 совпадают ее левая и правая производные:
совпадают ее левая и правая производные: 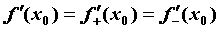 . .
ПРИМЕР 2 . Вычисление
односторонних производных
Секущая графика функции - Пусть 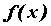 — функция, определенная на промежутке — функция, определенная на промежутке 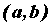 . Прямая, проходящая через точки . Прямая, проходящая через точки 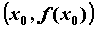 , , 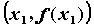 , , 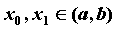 , , 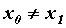 называется секущей графика функции называется секущей графика функции 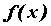 . Угловой коэффициент . Угловой коэффициент 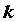 секущей
равен секущей
равен 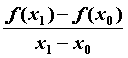 и ее уравнение имеет вид и ее уравнение имеет вид 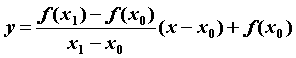 . .
ПРИМЕР 3 . Построение секущей
графика функции
Касательная и нормаль к графику функции
- Касательной к графику функции 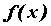 в точке в точке 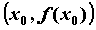 называется предельное
положение секущей, проходящей через точки называется предельное
положение секущей, проходящей через точки 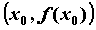 , , 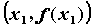 , когда , когда 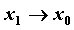 . Угловой
коэффициент касательной равен значению
производной в точке . Угловой
коэффициент касательной равен значению
производной в точке 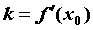 и ее
уравнение имеет вид и ее
уравнение имеет вид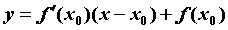 . Нормалью
к графику функции . Нормалью
к графику функции 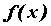 в точке в точке 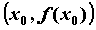 называется прямая , проходящая через эту
точку перпендикулярно касательной. Угловой
коэффициент нормали равен называется прямая , проходящая через эту
точку перпендикулярно касательной. Угловой
коэффициент нормали равен 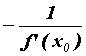 и ее
уравнение имеет вид и ее
уравнение имеет вид 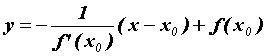 . .
ПРИМЕР 4. Построение
касательной и нормали к графику функции

|

