Основные
определения ~ Бесконечно большие
функции
Основные определения.
Рассмотрим функцию 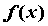 , определенную в
некоторой окрестности точки , определенную в
некоторой окрестности точки 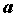 , , 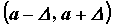 , ,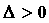 , за исключением, быть
может, самой точки , за исключением, быть
может, самой точки 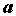 . Число . Число 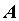 называется пределом функции
называется пределом функции 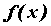 при при 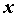 ,
стремящемся к ,
стремящемся к 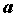 , если для любого положительного числа , если для любого положительного числа 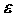 , как бы
мало оно ни было, существует такое положительное
число , как бы
мало оно ни было, существует такое положительное
число 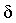 , что для всех
, что для всех 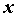 , удовлетворяющих
неравенству , удовлетворяющих
неравенству 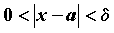 , справедливо
неравенство , справедливо
неравенство 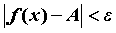 . Говорят “предел функции . Говорят “предел функции 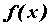 в точке в точке 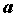 ” и
обозначают ” и
обозначают 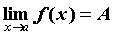 . Неравенство . Неравенство 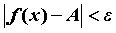 для всех для всех 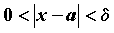 ,
эквивалентное неравенствам ,
эквивалентное неравенствам 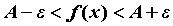 , , 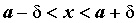 , означают, что для
любого , означают, что для
любого 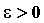 существует такое существует такое 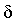 , что для , что для 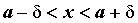 график
функции график
функции 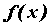 расположен на плоскости расположен на плоскости 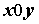 в
прямоугольнике в
прямоугольнике 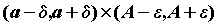 . При вычислениях на
компьютере мы имеем дело с дискретными
значениями переменных. Поэтому удобнее
пользоваться другим, эквивалентным
приведенному, определением предела. А именно: . При вычислениях на
компьютере мы имеем дело с дискретными
значениями переменных. Поэтому удобнее
пользоваться другим, эквивалентным
приведенному, определением предела. А именно: 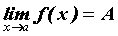 , если
для любой, сходящейся к , если
для любой, сходящейся к 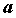 последовательности значений аргумента последовательности значений аргумента
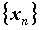 ,
соответствующая последовательность значений
функции ,
соответствующая последовательность значений
функции 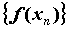 сходится к числу сходится к числу 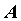 . Отсюда следует, в
частности, что для любого . Отсюда следует, в
частности, что для любого 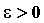 существует такое существует такое 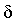 , что для
любой последовательности , что для
любой последовательности 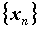 , сходящейся к , сходящейся к 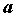 , точки с
координатами , точки с
координатами 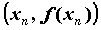 находятся на плоскости внутри
прямоугольника находятся на плоскости внутри
прямоугольника 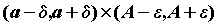 . .
ПРИМЕР 1 . Доказательство
существования предела функции в точке
Бесконечно большие функции.
Если для любой последовательности 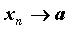 значений аргумента соответствующая
последовательность значений функции
значений аргумента соответствующая
последовательность значений функции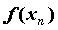 бесконечно большая, то функция
бесконечно большая, то функция 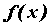 называется бесконечно
большой в точке называется бесконечно
большой в точке 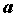 . Если . Если 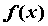 бесконечно большая в
точке бесконечно большая в
точке 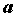 ,
то для любого положительного числа ,
то для любого положительного числа 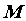 , как бы
велико оно ни было, существует такое число , как бы
велико оно ни было, существует такое число 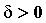 , что для
всех , что для
всех 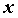 ,
удовлетворяющих неравенству ,
удовлетворяющих неравенству  , справедливо
неравенство , справедливо
неравенство 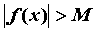 ; обозначают ; обозначают 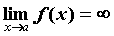 . .
ПРИМЕР 2 . Доказательство того,
что функция бесконечно большая
ПРИМЕР 3 . Функция, не имеющая
предела в точке
|

