Основные
определения ~ Бесконечно малая
последовательность ~ Бесконечно
большая последовательность
Основные определения. Последовательность
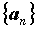 - это
функция, заданная на множестве натуральных чисел - это
функция, заданная на множестве натуральных чисел
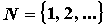 .
Число .
Число 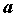 называется пределом последовательности
называется пределом последовательности 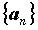 , если для
любого положительного числа , если для
любого положительного числа 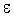 , как бы мало оно ни
было, существует такой номер , как бы мало оно ни
было, существует такой номер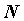 , что для всех , что для всех 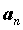 c
номерами c
номерами 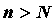 справедливо неравенство справедливо неравенство 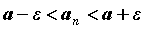 .
Неравенство .
Неравенство 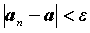 , эквивалентное неравенству , эквивалентное неравенству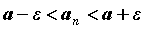 ,
означает, что для любого ,
означает, что для любого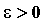 существует такой
номер существует такой
номер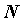 ,
что все ,
что все 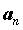 c номерами c номерами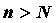 расположены между расположены между 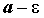 и и 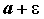 .
Последовательность, предел которой - конечное
число .
Последовательность, предел которой - конечное
число 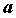 ,
называется сходящейся, и ее предел
обозначают ,
называется сходящейся, и ее предел
обозначают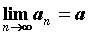 . Если изобразить элементы
последовательности . Если изобразить элементы
последовательности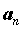 на плоскости точками с
координатами на плоскости точками с
координатами 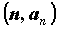 , то неравенства , то неравенства 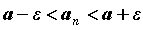 означают, что все
точки означают, что все
точки 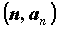 с номерами
с номерами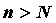 расположены между параллельными оси
абсцисс прямыми расположены между параллельными оси
абсцисс прямыми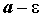 и и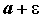 . .
ПРИМЕР 1 . Сходящаяся
последовательность
Бесконечно малая последовательность.
Последовательность 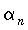 , предел которой равен
нулю , предел которой равен
нулю 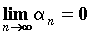 ,
называется бесконечно малой. ,
называется бесконечно малой.
ПРИМЕР 2 . Бесконечно малая
последовательность
Бесконечно большая последовательность.
Последовательность 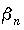 называется бесконечно
большой, если для любого положительного числа называется бесконечно
большой, если для любого положительного числа 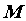 , как бы
велико оно ни было, существует такой номер , как бы
велико оно ни было, существует такой номер 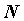 , что для
всех , что для
всех 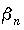 с
номерами с
номерами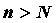 справедливо неравенство справедливо неравенство 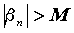 ,
записываем ,
записываем 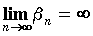 . .
ПРИМЕР 3 . Бесконечно большая
последовательность
ПРИМЕР 4 . Исследование процесса
сходимости последовательности

|

