Дифференцируемость
функции в точке ~ Дифференциал
функции ~ Связь дифференциала и
производной
Дифференцируемость функции в точке.
Пусть функция 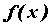 определена в
некоторой окрестности точки определена в
некоторой окрестности точки 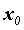 . Рассмотрим
приращение функции в этой точке: . Рассмотрим
приращение функции в этой точке: 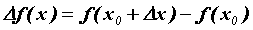 . Функция . Функция 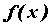 называется
дифференцируемой в точке , если ее приращение
можно записать в виде называется
дифференцируемой в точке , если ее приращение
можно записать в виде 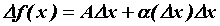 , где , где 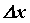 - приращение
независимой переменной, А – постоянная, не
зависящая от - приращение
независимой переменной, А – постоянная, не
зависящая от 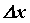 , , 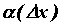 - бесконечно
малая функция при - бесконечно
малая функция при 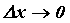 . .
ПРИМЕР 1 . Вычисление
приращения функции в точке
Дифференциал функции.
Дифференциалом функции 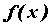 в точке в точке 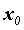 называется
линейная по называется
линейная по 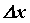 часть часть 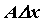 приращения приращения 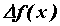 .
Дифференциал обозначается .
Дифференциал обозначается 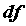 , то есть , то есть
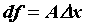 .
Рассматривая функцию .
Рассматривая функцию 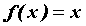 , нетрудно убедиться,
что , нетрудно убедиться,
что 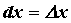 , если , если 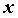 - независимая
переменная. - независимая
переменная.
ПРИМЕР 2 . Вычисление
дифференциала функции по определению
Связь дифференциала и производной.
Воспользуемся определением производной для дифференцируемой
функции 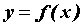 в точке в точке 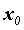 : : 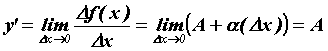 . Таким образом,
дифференциал функции выражается формулой . Таким образом,
дифференциал функции выражается формулой 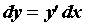 , то
есть для вычисления дифференциала необходимо
лишь вычислить производную и умножить ее на , то
есть для вычисления дифференциала необходимо
лишь вычислить производную и умножить ее на 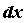 .
Поэтому часто слова “вычисление производной” и
“дифференцирование” считают синонимами. Для
того, чтобы функция была дифференцируема в точке,
необходимо и достаточно, чтобы в этой точке
существовала конечная производная. .
Поэтому часто слова “вычисление производной” и
“дифференцирование” считают синонимами. Для
того, чтобы функция была дифференцируема в точке,
необходимо и достаточно, чтобы в этой точке
существовала конечная производная.
ПРИМЕР 3 . Вычисление
дифференциала функции

|

