Понятие
бесконечно малой функции ~ Сравнение
бесконечно малых ~ Эквивалентные
бесконечно малые
Бесконечно малая функция.
Рассмотрим функцию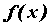 , определенную в
некоторой окрестности , определенную в
некоторой окрестности 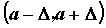 точки точки 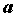 , , 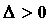 , за
исключением, быть может, самой точки , за
исключением, быть может, самой точки 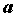 .
Функция .
Функция 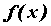 называется бесконечно малой при называется бесконечно малой при 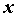 ,
стремящемся к ,
стремящемся к 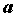 , если , если 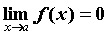 . Если . Если 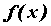 —
бесконечно малая в точке —
бесконечно малая в точке 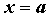 , то для любого
положительного числа , то для любого
положительного числа 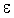 , как бы мало оно ни
было, существует такое положительное число , как бы мало оно ни
было, существует такое положительное число 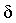 , что
для всех , что
для всех 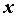 , удовлетворяющих неравенству , удовлетворяющих неравенству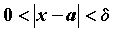 ,
справедливо неравенство ,
справедливо неравенство 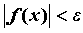 . Неравенства . Неравенства 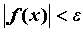 для
всех для
всех 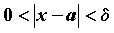 ,
эквивалентные неравенствам ,
эквивалентные неравенствам 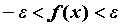 , , 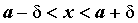 , означают, что для
любого , означают, что для
любого 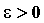 существует такое существует такое 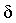 , что для , что для 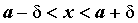 график
функции расположен на плоскости в
прямоугольнике график
функции расположен на плоскости в
прямоугольнике 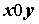 . Важно, что слова “за исключением, быть
может, самой точки ” означают, что нас не
интересует сама эта точка. Это можно понять, если
рассмотреть функцию . Важно, что слова “за исключением, быть
может, самой точки ” означают, что нас не
интересует сама эта точка. Это можно понять, если
рассмотреть функцию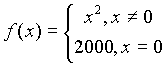 . При x,
стремящемся к нулю, функция-таки стремится к
нулю, независимо от того, какое значение она
принимает в точке x=0. Следовательно, предел равен нулю и
функция является бесконечно малой. . При x,
стремящемся к нулю, функция-таки стремится к
нулю, независимо от того, какое значение она
принимает в точке x=0. Следовательно, предел равен нулю и
функция является бесконечно малой.
ПРИМЕР 1 . Бесконечно малые
функции
Сравнение бесконечно малых функций.
Пусть 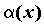 и и 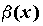 — две функции, бесконечно малые в
точке — две функции, бесконечно малые в
точке 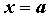 .
Если .
Если 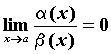 ,
то говорят, что ,
то говорят, что 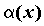 более высокого порядка малости, чем более высокого порядка малости, чем 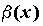 и
обозначают и
обозначают 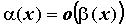 . Если же . Если же 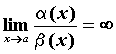 , то , то 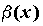 более высокого
порядка малости, чем более высокого
порядка малости, чем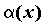 ; обозначают ; обозначают 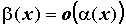 .
Бесконечно малые функции .
Бесконечно малые функции 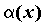 и и 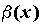 называются бесконечно
малыми одного порядка малости, если называются бесконечно
малыми одного порядка малости, если 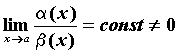 ,
обозначают ,
обозначают 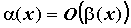 . И, наконец, если . И, наконец, если 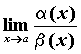 не
существует, то бесконечно малые функции не
существует, то бесконечно малые функции 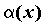 и и 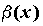 несравнимы.
несравнимы.
ПРИМЕР 2 . Сравнение
бесконечно малых функций
Эквивалентные бесконечно малые функции.
Если 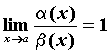 , то бесконечно малые функции , то бесконечно малые функции 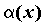 и и 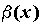 называются эквивалентными, обозначают
называются эквивалентными, обозначают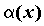 ~ ~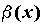 . .
ПРИМЕР 3 . Таблица
эквивалентных бесконечно малых функций

|

