Решение системы ~ Задача Коши ~ Интегральная кривая ~ Теорема существования и единственности ~ Численное решение задачи Коши

Рассмотрим систему дифференциальных уравнений
y'₁ = f₁(x, y₁, y₂ , ..., y_n),
y'₂ = f₂ (x, y₁, y₂ , ..., y_n),
..............................
y'_n = f_n (x, y₁, y₂ , ..., y_n),
где x — независимая переменная, а
y₁(x), y₂(x), ..., y_n(x) — неизвестные функции, n — порядок системы.

Обозначив
 
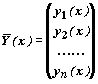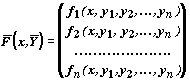
запишем систему в векторной форме
`Y '=`F(x,`Y ).

Решением системы называется вектор-функция `Y , которая определена и нерерывно дифференцируема на интервале (a, b) и удовлетворяет системе, т.е. для всех x<sub>0</sub>О (a, b) справедливо
`Y '(x) =`F(x,`Y (x)).

Задачей Коши (задачей с начальными условиями) называется следующая задача: найти такое решение`Y (x) системы `Y '=`F(x,`Y ), что `Y (x<sub>0</sub>) =`Y ₀,
где x₀ — заданное число, а `Y ₀ — заданный вектор.

Интегральной кривой системы называется кривая в (n+1) -мерном пространстве Rⁿ⁺¹_x,y,  заданная уравнением `Y =`Y (x), где `Y (x) - решение системы.Таким образом, решить задачу Коши — это значит найти интегральную кривую, проходящую через заданную точку пространства Rⁿ⁺¹_x,y.

Для нормальных систем обыкновенных дифференциальных уравнений справедлива следующая теорема существования и единственности решения задачи Коши.

Если вектор-функция `F(x,`Y (x)) и ее частные производные по переменным y_i , i = 1, 2, ..., n, непрерывны в области G пространства Rⁿ⁺¹_x,y, то на некотором интервале (x₀ -h, x₀+h) существует единственное решение системы
`Y '(x) =`F(x,`Y (x)) ,
удовлетворяющее начальному условию
`Y (x₀) =`Y ₀,
т.е. через каждую точку области G проходит единственная интегральная кривая системы.

Подробнее геометрическая интерпретация систем обыкновенных дифференциальных уравнений и их решений рассмотрена в разделе, посвященном изучению автономных систем.

ПРИМЕР 1. Интегральная кривая для системы дифференциальных уравнений 2-го порядка.

Если задачу об отыскании всех решений системы дифференциальных уравнений удается свести к конечному числу алгебраических операций, операций интегрирования и дифференцирования известных функций, то говорят, что система интегрируется в квадратурах.
В приложениях крайне редко встречаются системы, интегрируемые в квадратурах. Поэтому для исследования дифференциальных уравнений широко используются приближенные, численные методы их решения.

Численное решение задачи Коши для системы обыкновенных дифференциальных уравнений состоит в построении таблицы приближенных значений
y_i,1, y_i,2 , ..., y_i,N   компонент y_i(x_j,) вектора решения `Y (x) в точках
x₁, x₂ , ..., x_N.

Чтобы получить расчетные формулы метода Рунге—Кутты для систем дифференциальных уравнений, достаточно в расчетных формулах для уравнений первого порядка заменить
y, f(x, y), k₁, k₂, k₃ , k₄ на
`Y , F(x,`Y ), `k <sub>1</sub>, `k ₂, `k <sub>3</sub>, `k ₄.

ПРИМЕР 2. Численное решение задачи Коши для системы дифференциальных уравнений 2-го порядка методом Рунге-Кутты. Графики чтсленного решения.

Задача Коши для любого дифференциального уравнения n -го порядка 
y⁽ⁿ⁾ = f(x, y' , y' , ..., y^(n-1)),
y(x₀ )= y₀ , y'(x₀ )= y_0,1, y''(x₀ )= y_0,2 , ..., y^(n-1)(x₀ )= y_0,n-1
легко сводится к задаче  для системы дифференциальных уравнений порядка
`Y '=`F(x,`Y ), где

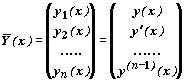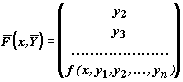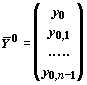
ПРИМЕР 3. Сведение задачи Коши для дифференциального уравнения 2-го порядка к задаче Коши для системы  дифференциальных уравнений 2-го порядка.