© 2000 Seattle Central Community College публикуется с разрешения

(38 Кб, Maple)

06. 01  Параметрические уравнения

• Пример 01

Упражнение 6.1

• Учебная площадка 6.1
• Ответ 6.1

06. 02  Построение графиков неявных функций

• Пример 01
• Пример 02

Упражнение 6.2

• Учебная площадка 6.2
• Ответ 6.2

06. 03  Построение графиков в полярной системе координат

06. 04  Опции графических команд

06. 01 Параметрические уравнения

* Parametric Equations *

Maple-команда plot может использоваться и для построения кривых, заданных параметрически.

В таком случае линии задаются двумя параметрическими уравнениями x=f(t) и y=g(t), а параметру t придаются значения из отрезка [a,b] . Советуем применить команду

plot( [ f(t) , g(t) , t=a..b] , x=xmin..xmax, y=ymin..ymax);

Здесь есть два обстоятельства, на которые следует обратить особое внимание. 1). В квадратных скобках стоят три элемента: два параметрических выражения для x и y и область изменения параметра t . 2). И в данном случае активизируется окно просмотра на графической панели для определения координат (х;у) любой точки линии (то есть для x=xmin..xmax, y=ymin..ymax ) .

Пример 01

Построим линию, заданную параметрически: , если t принадлежит отрезку [-2;2].

> plot([t^2-t,2*t-t^3,t=-2..2],x=-2..5,y=-5..5);

Упражнение 6.1

Построить линию, заданную параметрически: , если t принадлежит отрезку [0;2 ].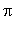

Учебная площадка 6.1

>

>

>

Ответ 6.1

> plot([sin(3*t),sin(4*t),t=0..2*Pi],x=-2..2,y=-2..2);

06. 02 Построение графиков неявных функций

* Implicit Plots *

Maple может строить графики функций, заданных неявно ( в виде уравнения относительно х и у ) .

Пример 01

Для построения гиперболы, заданной уравнением, не разрешенным относительно у , следует воспользоваться командой implicitplot . В отличие от команды plot , на сей раз обязательно подключение библиотеки plots :

> with(plots):

Warning, the name changecoords has been redefined

На данном примере попробуйте запомнить основные компоненты команды:

> implicitplot(x^2/4-y^2/4=1,x=-5..5,y=-5..5);

Пример 02

Построим с помощью команды implicitplot эллипс .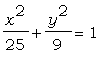

Напомним, что из этого канонического уравнения следует, что большая полуось эллипса равна 5, а малая - 3.

Попробуем по аналогии:

> implicitplot(x^2/25+y^2/9=1,x=-5..5,y=-5..5);

Как ни странно, попытка может показаться неудачной! Вместо эллипса, не исключено, появится изображение окружности. Напомним, что Maple, по умолчанию, самостоятельно подбирает масштабы осей координат. Чтобы рисунок был качественно верным, в команду implicitplot следует вставить (через запятую) опцию scalling=constrained , задающую равенство масштабов по х и у :

> implicitplot(x^2/25+y^2/9=1,x=-5..5,y=-5..5,scaling=constrained);

Упражнение 6.2

Построить график уравнения .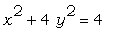

Учебная площадка 6.2

>

>

>

>

>

>

Ответ 6.2

> implicitplot(x^2+4*y^2=4,x=-3..3,y=-2..2,scaling=constrained);

06. 03 Построение графиков в полярной системе координат

* Polar Graphs * (optional)

Построение графиков полярных уравнений 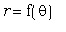осуществляется при помощи команды polartplot из того же графического пакета. В этом разделе мы уже прибегали к помощи пакета plots . Но если в процессе работы Вы впервые используете его содержимое, обязательно обращение

> with(plots):

Приведём несколько примеров, причём во всех случаях добавим опцию scalling=constrained , чтобы изображение было геометрически верным.

> polarplot(1+cos(theta),theta=-Pi..Pi,scaling=constrained);

> polarplot(sin(3*theta),theta=-Pi..Pi,scaling=constrained);

06. 04 Опции графических команд

* Plot Options *

При использовании графических команд, таких как plot , в Maple предусмотрено большое количество опций, позволяющих улучшать качество рисунка.Чтобы получить развёрнутую справку по их применению, выполните обращение к Help'у системы Maple:

> ?plot[options];