| © 2000
Seattle Central Community College
публикуется с разрешения |
![[Maple OLE 2.0 Object]](../0/images/01.gif) ![[Maple OLE 2.0 Object]](../0/images/02.gif) |
 (48 Кб,
Maple) (48 Кб,
Maple)
 
В этом разделе Вы познакомитесь с
основными приёмами построения графиков
выражений. Кроме того, Вы узнаете: как в одной
системе координат построить сразу несколько
графиков; как наносить точки; как комбинировать
графические объекты различной природы.
03. 01 Построение графиков
выражений. Команда plot
Упражнение 3.1
Упражнение 3.2
03. 02 Одновременное
построение нескольких график
Упражнение 3.3
03. 03 Изображение точек на
рисунке
Упражнение 3.4
03. 04 Вывод комбинации
графических объектов: команда display
Упражнение 3.5
* Plotting an Expression: the plot command *
Пример 01
Воспользуемся командой plot для
построения графика функции 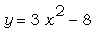 на отрезке [-5;5]. на отрезке [-5;5].
> plot(3*x^2-8,x=-5..5);
![[Maple Plot]](images/34.gif)
Обратите внимание, что Maple
самостоятельно выбирает масштаб для оси Оу: для
него важно, чтобы на графике уместилась вся линия
.
Вы можете вмешаться в этот процесс, если
лично дополните команду ещё и диапазоном
изменения ординаты графика. Например, указав
отрезок [-20;40] , как это сделано ниже:
> plot(3*x^2-8,x=-5..5,y=-20..40);
![[Maple Plot]](images/35.gif)
Если Вы щёлкните левой кнопкой по
графику, то вверху документа дополнительно
появится графическая панель . В верхнем
левом окошке этой панели будут выводиться
координаты точки, отвечающей месту расположения
курсора на графике. Если нажать на кнопку панели
" 1 : 1 ", то Maple представит график для
случая, когда масштабы осей абсцисс и ординат
совпадают.
Активизировав рисунок курсором,
поэкспериментируйте с другими кнопками панели!
Компьютер не сломается!
Пример 02
Автоматическое масштабирование полезно
в том случае, когда Вы не в состоянии предсказать
множество значений функции. В некоторых случаях
эта особеность Maple просто противопоказана
качеству изображения. Например, это относится к случаю
графиков с вертикальными асимптотами . И тогда
чрезвычайно желательно лично указать
промежуток изменения ординат точек графика.
Сравним два графика. Обратите внимание,
как именно во вторую команду plot встраивается
указание диапазона изменений у:
> plot(x/(x-2),x=-5..5);
![[Maple Plot]](images/36.gif)
> plot(x/(x-2),x=-5..5,y=-20..20);
![[Maple Plot]](images/37.gif)
Пример 03
Построим график функции 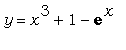 ,
ограничившись областью определения [-8;8].
Подберём такое множество значений функции, чтобы
увидеть все 4 её корня ( the x-intercepts ). ,
ограничившись областью определения [-8;8].
Подберём такое множество значений функции, чтобы
увидеть все 4 её корня ( the x-intercepts ).
Но вначале выполним построение с
автомасштабированием оси Оу:
> plot(x^3+1-exp(x),x=-8..8);
![[Maple Plot]](images/39.gif)
Видим: вблизи точки х = 8 отрицательные
значения функции резко растут по абсолютной
величине. Из-за этого очень тяжело разобраться
даже в том, сколько корней имеет функция, не
говоря уже об оценке этих корней.
Теперь определим границы у-промежутка:
> plot(x^3+1-exp(x),x=-8..8,y=-5..15);
![[Maple Plot]](images/310.gif)
Построить график функции y = sin x
на промежутке длиною в 2 наименьших
положительных её периода.
Учебная площадка 3.1
>
>
>
>
Ответ 3.1
> plot (sin(x),x=-2*Pi..2*Pi);
![[Maple Plot]](images/311.gif)
Постройте график функции 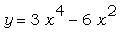 на отрезке [-10;10]
с автомасштабированием по у. Внимательно изучите
полученный рисунок и подберите диапазоны
изменения абсцисс и ординат так, чтобы можно было
легко определить количество корней функции. При
помощи мыши прикиньте координаты этих корней.. на отрезке [-10;10]
с автомасштабированием по у. Внимательно изучите
полученный рисунок и подберите диапазоны
изменения абсцисс и ординат так, чтобы можно было
легко определить количество корней функции. При
помощи мыши прикиньте координаты этих корней..
Учебная площадка 3.2
>
>
>
>
Ответ 3.2
> plot(3*x^4-6*x^2,x);
![[Maple Plot]](images/313.gif)
Обратите внимание : при стремлении
аргумента к точкам -10 и 10 значения функции резко
растут. Автомасштабирование приводит к тому, что
можно ошибочно говорить о наличии всего лишь
одного корня у функции, х = 0. Поэтому в следующей
команде уделим внимание значениям аргумента,
достаточно близким к х = 0:
> plot (3*x^4-6*x^2,x=-3..3,y=-5..15);
![[Maple Plot]](images/314.gif)
Скользя мышью вдоль оси Ох, благодаря
окну графической панели, определим примерные
значения корней функции: ![x[1] = -1.4](images/315.gif) ![x[2] = 0](images/316.gif) , , ![x[3] = 1.4](images/317.gif) . .
* Plotting Several Expressions *
Чтобы построить несколько графиков в
одной системе координат, в команде plot
необходимо записать функциональные выражения в
виде списка, т.е. с использованием квадратных
скобок через запятую: [f(x), g(x),h(x)] . Однако, можно
использовать и фигурные скобки:
> plot([cos(x),x^2],x=-1..4,y=-4..4);
![[Maple Plot]](images/318.gif)
> plot({cos(x),x^2},x=-1..4,y=-4..4);
![[Maple Plot]](images/319.gif)
Обратите внимание: сколько графиков -
столько и цветов, которые Maple подбирает по своему
усмотрению. Но можно и самостоятельно указать
цвет для каждого графика, добавляя, через
запятую, опцию цвета внутри команды plot
(типа: color=red ).
Напомним, что мы хотим построить сразу
несколько графиков. Установка цвета поэтому
также должна осуществляться в виде списка,
заключенного в квадратные скобки:
> plot([cos(x),x^2],x=-1..5,y=-4..4,color=[blue,black]);
![[Maple Plot]](images/320.gif)
В Вашем распоряжении 25 цветов: аквамарин
(зеленовато-голубой, aquamarine ), чёрный ( black ),
синий ( blue ), морская волна ( navy ), коралл ( coral
), изумруд( cyan ), коричневый ( brown ), золотой ( gold
), зелёный( green ), серый( gray ), серый( grey ),
хаки ( khaki ), магента ( magenta ), марон ( maroon
), оранжевый ( orange ), розовый( pink ), слива ( plum
), красный ( red ), сьенна ( sienna ), загар( tan
), бирюзовый ( turquoise ), фиолетовый ( violet ),
пшеничный ( wheat ), белый ( white ), жёлтый( yellow
).
Постройте в одной системе координат
графики функций 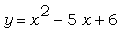 и и 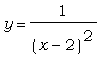 . Поэкспериментируйте с
диапазонами изменения абсцисс и ординат так,
чтобы графики легко "читались". . Поэкспериментируйте с
диапазонами изменения абсцисс и ординат так,
чтобы графики легко "читались". 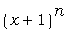
Учебная площадка 3.3
>
>
>
>
>
>
>
Ответ 3.3
> y1:=x^2-5*x+6;
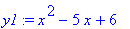
> y2:=1/(x-2)^2;
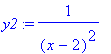
> plot([y1,y2],x=-3..8,y=-1..6);
![[Maple Plot]](images/326.gif)
* Plotting points *
Команда plot может привязывать к
системе координат и отдельно взятые точки.
Пример 01
Изобразим на плоскости точку с
координатами (2;3):
> plot([ [2,3] ],style=point);
![[Maple Plot]](images/327.gif)
Обратите внимание на использование
квадратных скобок.
Пример 02
Как и ранее, мы можем контролировать
диапазон изменения абсцисс и ординат:
> plot([ [2,3] ],x=-7..7,y=-7..7,style=point);
![[Maple Plot]](images/328.gif)
Пример 03
Для нанесения на плоскость сразу
нескольких точек, в команду plot следует
встроить список их координат:
> plot([ [2,3],[-2,5],[1,-4]
],x=-7..7,y=-7..7,style=point);
![[Maple Plot]](images/329.gif)
Обратите внимание на использование
запятых и квадратных скобок.
Пример 04
Если в предыдущем примере стиль " point
" изменить на " line ", то Maple изобразит
ломаную, соединяющую указанные точки:
> plot([ [2,3],[-2,5],[1,-4] ],x=-7..7,y=-7..7,style=line);
![[Maple Plot]](images/330.gif)
Пример 05
Кроме всего прочего, Вы можете опционно
указать цвет и символ, посредством которых
отмечается на плоскости точка (алмаз( diamond ),
круг ( circle ), а по умолчанию - крестик ( cross )):
> plot([[3,2],[-2,3],[2,-1]],style=point,color=blue,symbol=circle);
![[Maple Plot]](images/331.gif)
Изобразить на плоскости точки с
координатами: [1,4], [-2,-3],[-4,-5] и [-6,5]. . Используйте
при этом красный цвет и "алмаз" в качестве
символа вывода.
Учебная площадка 3.4
>
>
>
>
>
>
>
Ответ 3.4
> plot([[1,4],[-2,-3],[4,-5],[-6,5]],style=point,color=red,symbol=diamond);
![[Maple Plot]](images/332.gif)
> plot([[1,4],[-2,-3],[4,-5],[-6,5]],style=line,color=red,symbol=diamond);
![[Maple Plot]](images/333.gif)
* Combining Graphs of Expressions and Points: the display command
*
Графический пакет plots , куда включена
команда plot , содержит много дополнительных
возможностей. Чтобы использовать команды пакета,
вначале нужно обратиться к самому пакету:
> with(plots):
Warning, the name changecoords has been redefined
А если строку завершить точкой с
запятой, то Maple выведет полный список
содержащихся в пакете команд:
> with(plots);
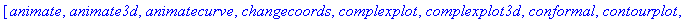
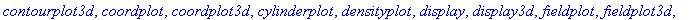
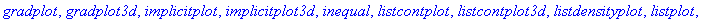

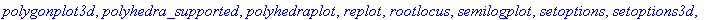
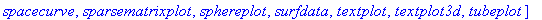
Специальная команда display позволяет
одновременно, в одних и тех же осях координат,
выводить графические объекты различной природы.
Чтобы ею воспользоваться, каждому графическому
объекту нужно присвоить имя, каждую строку
присваивания закончить двоеточием, а саму
команду завершить символом " точка с запятой
". (В случае завершения команды двоеточием, Maple
построит график лишь "в уме"):
> pict1:=plot([-3*x+5,9-x^2],x=-3..5,color=[green,red]):
> pict2:=plot([[-1,8],[4,-7]],style=point,color=blue,symbol=circle):
> display([pict1,pict2]);
![[Maple Plot]](images/340.gif)
Альтернативный вариант : объединить
все команды в одну группу выполнения, нажимая [ Shift
] - [ Enter ] в конце ввода каждой командной
строки.
> pict1:=plot([-3*x+5,9-x^2],x=-3..5,color=[green,red]):
> pict2:=plot([[-1,8],[4,-7]],style=point,color=blue,symbol=circle):
> display([pict1,pict2]);
![[Maple Plot]](images/341.gif)
Для более полной информации по этому
вопросу смотрите " Группы выполнения с более
чем одной командой " в Заметках об
интерфейсе Maple Worksheet.
Вывести график функции 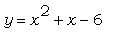 и на нём кружками
отметить точки пересечения с осями Ох и Оу. и на нём кружками
отметить точки пересечения с осями Ох и Оу.
Учебная площадка 3.5
>
>
>
>
>
>
>
Ответ 3.5
> pict4:=plot(x^2+x-6,x=-5..4,y=-8..8):
> pict5:=plot([[0,-6],[-3,0],[2,0]],style=point,symbol=circle,
color=blue):
> display([pict4,pict5]);
![[Maple Plot]](images/343.gif)
  
|

