| © 2000
Seattle Central Community College
публикуется с разрешения |
![[Maple OLE 2.0 Object]](../0/images/01.gif) ![[Maple OLE 2.0 Object]](../0/images/02.gif) |
 (51 Кб,
Maple) (51 Кб,
Maple)
 
В этом разделе Вы научитесь применять
команду solve для нахождения точных корней
уравнений (если это возможно). Из своего опыта Вы
знаете, что далеко не каждый тип уравнений имеет
точные корни. В таких случаях интересуются
приближенным численным решением. И у Maple для
этого имеется соответствующая команда - fsolve .
Кроме того, в этом разделе мы получим опыт
решения систем линейных уравнений.
04. 01 Преобразование
уравнений. Команды lhs и rhs
04. 02 Нахождение точных
корней. Команда solve
Упражнение 4.1
04. 03 Поиск приближенных
корней. Команда fsolve
Упражнение 4.2
Упражнение 4.3
Упражнение 4.4
04. 04 Решение уравнений в
общем виде
Упражнение 4.4
Упражнение 4.5
04. 05 Решение систем
линейных уравнений, используя команду solve
Упражнение 4.6
04. 06 Решение систем
линейных уравнений с избытком неизвестных
Упражнение 4.7
* Entering and Manipulating Equations: The lhs and
rhs commands *
Пример 01
Напомним, что уравнению, точно так же как
и выражению, можно присвоить имя. В следующей
командной строке мы введём уравнение 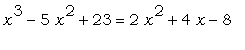 и присвоим ему имя " eq1 " : и присвоим ему имя " eq1 " :
> eq1:=x^3-5*x^2+23=2*x^2+4*x-8;
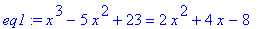
Пример 02
Мы можем вывести на экран левую и правую
части уравнения по-отдельности при помощи команд
lhs и rhs :
> lhs(eq1);
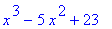
> rhs(eq1);
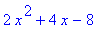
Пример 03
Воспользуемся командами lhs и rhs
для того, чтобы привести уравнение к
стандартному виду, в котором все члены собраны
слева, а справа остался только 0:
> eq2:=lhs(eq1)-rhs(eq1)=0;
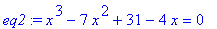
* Finding Exact Solutions: The solve command *
Рассмотрим вначале рациональные
уравнения. Известно, что существуют алгоритмы
определения точных корней рациональных корней
вплоть до 4-го порядка включительно. В Maple-команду solve
и заложены эти алгоритмы.
Пример 01
Воспользуемся командой solve для
нахождения точных корней кубического уравнения 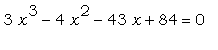 :
:
> solve(3*x^3-4*x^2-43*x+84=0,x);
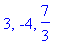
Обратите внимание: в команде мы
указываем, относительно какой переменной
следует решать уравнение. Хотя в нашем
конкретном случае это и не обязательно:
> solve(3*x^3-4*x^2-43*x+84=0);
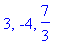
Maple нашел все 3 действительных корня и
вывел их ( в неупорядоченном виде ).
Пример 02
Иногда очень важно выбрать конкретный
корень, чтобы потом использовать в дальнейших
преобразованиях именно его. Для этого заранее
следует присвоить имя результату исполнения
команды solve . Назовём его X . Тогда
конструкция X[1] будет соответствовать
первому корню из списка (подчеркнем: это не
обязательно меньший корень! ), X[2] - второму
корню, и т.д. ( Скобки - квадратные! ):
> X:=solve(x^2-5*x+3=0,x);
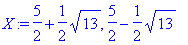
> X[1];
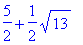
Посмотрите, однако, что будет выведено в
результате выполнения похожей команды:
> x[1]=%;
![x[1] = 5/2+1/2*sqrt(13)](images/413.gif)
Пример 03
Ещё раз подчеркнём: практика показывает,
что уравнению целесообразно присвоить имя.
Традиционно в Maple такое имя начинается с букв eq
:
> eq1:=7*x^3-11*x^2-27*x-9=0;
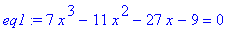
(Не путать оператор присваивания " :=
" со знаком равенства " = " !)
Теперь решим уравнение при помощи
команды solve . Множеству корней присвоим имя X
:
> X:=solve(eq1,x);
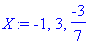
Для убедительности проверим, нет ли
среди найденных корней посторонних. Проверку
выполним непосредственной подстановкой
> subs(x=X[1],eq1);
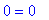
> subs(x=X[2],eq1);
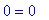
> subs(x=X[3],eq1);
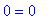
Пример 04
Разумеется, частенько "точные"
решения довольно громоздки, если не сказать
иначе. Например, это касается уравнения 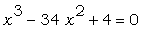 : :
> eq1:=x^3-34*x^2+4=0;
> X:=solve(eq1,x);
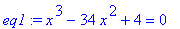
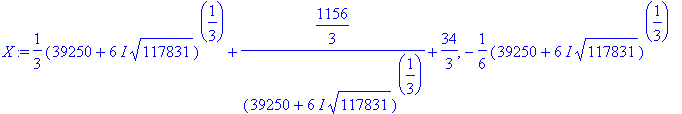
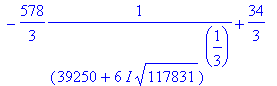
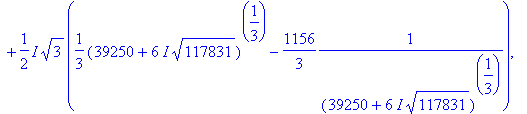
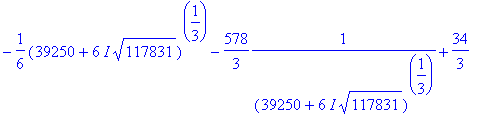
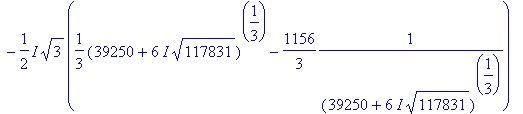
Теперь Вам понятно, о чем речь? Для себя
заметьте, что мнимая единица 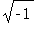 в Maple обозначается
посредством прописной буквы I .
Разумеется, в таких случаях не грех найти
приближенные значения корней. Имея на руках
точное решение, Вы и сами сообразите, как это
сделать: в Maple обозначается
посредством прописной буквы I .
Разумеется, в таких случаях не грех найти
приближенные значения корней. Имея на руках
точное решение, Вы и сами сообразите, как это
сделать:
> evalf(X);
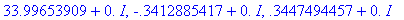
В подобных ситуациях хорошей
альтернативой команде solve является fsolve ,
особенности которой будут рассмотрены в
следующем параграфе.
Команда solve используется при
отыскании точных решений не только рациональных
уравнений. Ниже приведено несколько тому
иллюстраций. Но для многих типов иррациональных,
показательных, логарифмических,
тригонометрических и даже рациональных
уравнений точное решение искать бесполезно. На
помощь призывается команда fsolve .
Пример 05
Решим уравнение 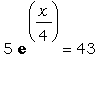 : :
> solve(5*exp(x/4)=43,x);
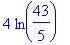
Пример 06
Иногда (а в тригонометрии - всегда
) Maple, по умолчанию , не выводит всё множество
корней:
> solve(sin(x)=1/2,x);
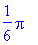
Но безвыходных ситуаций не бывает! Взяв
за основу полученный результат, воспользуйтесь
своими знаниями тригонометрических уравнений и
запишите полное решение ( как ? ).
Решить уравнение 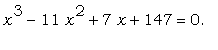 Разберитесь,
сколько различных корней имеет уравнение. Как Maple
поступает при наличии равных корней? Разберитесь,
сколько различных корней имеет уравнение. Как Maple
поступает при наличии равных корней?
Совет : разложите на множители левую
часть уравнения.
Учебная площадка 4.1
>
>
>
>
>
Ответ 4.1
> solve(x^3-11*x^2+7*x+147=0,x);
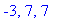
> factor(x^3-11*x^2+7*x+147);
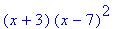
Корень х = 7 является двукратным, а потому
у кубического уравнения только два различных
корня. Разложение на множители левой части
уравнения - тому подтверждение.
* Finding Approximate Solutions: The fsolve command *
Для приближенного решения уравнений
используется Maple-команда fsolve . В случае
рационального уравнения, fsolve выводит весь
список действительных корней (см. Пример 01). Для
трансцендентных уравнений эта команда, по
умолчанию, выводит только один корень (см.
Примеры 02 и 03).
Пример 01
При помощи fsolve найдём приближенные
значения сразу всех четырёх действительных
корней рационального уравнения 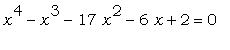 : :
> eq:=x^4-x^3-17*x^2-6*x+2=0;
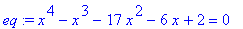
> fsolve(eq,x);
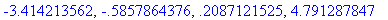
Эти четыре корня и составляют
исчерпывающее решение исходного рационального
уравнения ( хотя и приближенное ).
Пример 02
Используя команду fsolve , найти хотя
бы один действительный корень уравнения 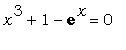 : :
> eq:=x^3+1-exp(x)=0;
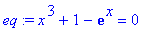
> fsolve(eq,x);
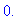
Maple и вывел только один корень. На этот
раз Maple не стал "живописать". Как теперь
убедиться в том, что других действительных
корней нет? Следующий пример даёт такой
инструментарий.
Пример 03
Получить все действительные
корни уравнения 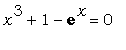 и убедиться в этом. и убедиться в этом.
Шаг первый ( Основная идея
) : найдём графическое решение уравнения. Для
этого построим график функции, стоящей в левой
части уравнения. Абсциссы точек пересечения
этого графика с осью Ох и будут искомыми корнями.
> plot(x^3+1-exp(x),x=-3..5,y=-5..15);
![[Maple Plot]](images/441.gif)
Т.к. мы умело подобрали диапазоны
изменений абсцисс и ординат точек графика, то
легко обнаружим 4 точки пересечения линии с
осью Ох. Одна из них соответствует корню,
найденному в Примере 02 ( какая именно? ).
Второй корень очевиден: х = 0. А как
поточнее найти остальные?
Шаг второй ( Уточнение )
: применим команду fsolve более "зряче". В
Maple предусмотрена возможность указания
промежутка, на котором отыскиваются корни. В
частности, для определения отрицательного корня
нашего уравнения, укажем, что поиски следует
вести в "районе" [-1;-0.2]. Об этом красноречиво
свидетельствует графическое решение.
> fsolve(eq,x=-1..-.2);
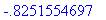
Оставшиеся корни явно принадлежат
промежуткам [1;2] и [4;5] . Расскажем об этом команде fsolve
:
> fsolve(eq,x=1..2);
fsolve(eq,x=4..5);
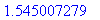
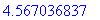
Ну а что произойдёт, если мы подсунем Maple
"пустой участок"? Например, отрезок [2;4] для
нашего уравнения. Там графического решения явно
нет:
> fsolve(eq,x=2..4);
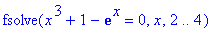
Maple выдаёт название команды, само
уравнение, имя аргумента и отрезок. Т.е. ничего
нового. Мол: "Ищите корни сами, а я не нашел".
Шаг третий ( Дополнительный
анализ ) : Как теперь удостовериться в том,
что найдены все корни , а не только в видимой
области графического решения? Для этого следует
расширить интервал поисков:
> plot(x^3+1-exp(x),x=-3..50,y=-10..15);
![[Maple Plot]](images/446.gif)
Новых точек пересечения нет. В конце
концов мы понимаем, что экспоненциальное
слагаемое на границах промежутка вносит самый
существенный вклад в величину функции из левой
части уравнения. Значения функции в этой области
стремятся к 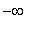 , а потому дополнительных корней нам не
найти. , а потому дополнительных корней нам не
найти.
Попробуем в других местах: справа и
слева от области найденных корней.
> fsolve(eq,x=5..50);
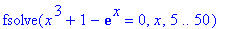
> fsolve(eq,x=-50..-1);
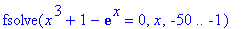
И здесь ни одного дополнительного корня!
Поняв, что с влиянием показательной части
уравнения всё ясно, делаем окончательные выводы.
Исчерпывающее решение уравнения 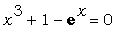 состоит из четырёх корней: -.8251554597 , 0 , 1.545007279 ,
4.567036837 .
состоит из четырёх корней: -.8251554597 , 0 , 1.545007279 ,
4.567036837 .
Пример 04
Применим команду fsolve для
приближенного решения трансцендентного
уравнения 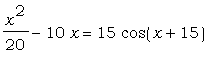 . .
Как и в предыдущем случае, найдём
вначале качественное графическое решение. Для
этого ещё нужно угадать, как разбросать по обеим
частям уравнения его члены. Но графические
возможности Maple настолько великолепны, что почти
всегда можно собирать все члены уравнения с
одной стороны.
Рассмотрим уравнение, равносильное
данному: 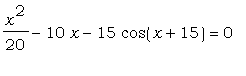 . Абсциссы точек
пересечения графика функции, стоящей в левой
части уравнения, с осью Ох и будут искомыми
корнями. . Абсциссы точек
пересечения графика функции, стоящей в левой
части уравнения, с осью Ох и будут искомыми
корнями.
> eq:=x^2/20-10*x-15*cos(x+15)=0;
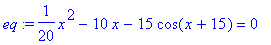
> plot(lhs(eq),x=-10..10);
![[Maple Plot]](images/454.gif)
График указывает область поисков
корней: промежуток [1;2]. Настаёт черёд команды fsolve
:
> fsolve(eq,x=1..2);
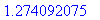
Корень найден. Но, очевидно, он - не
единственный. Расширьте область поисков и ещё
раз примените команду fsolve для отыскания
второго корня.
Найти все действительные корни
уравнения 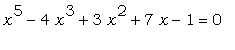 , начав с графического
решения. , начав с графического
решения.
Учебная площадка 4.2
>
>
>
>
>
Ответ 4.2
Построим график левой части уравнения:
> eq:=x^5-4*x^3+3*x^2+7*x-1=0;
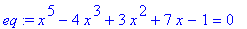
> plot(lhs(eq),x=-5..5,y=-5..5);
![[Maple Plot]](images/458.gif)
В результате находим корни уравнения в
первом приближении: -2 ; -1.5 ; 0 . Применим теперь
команду fsolve без указания диапазона поиска ( оценим
возможности Maple ):
> fsolve(eq,x);
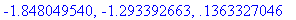
С удовлетворением отмечаем, что Maple
выводит все три корня (Не будем забывать, что
решали рациональное уравнение.)
Найти все корни уравнения 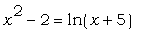 .
Воспользуйтесь графическим решением. Проверьте
каждый корень непосредственной подстановкой. .
Воспользуйтесь графическим решением. Проверьте
каждый корень непосредственной подстановкой.
Учебная площадка 4.3
>
>
>
>
>
>
>
Ответ 4.3
Приведём уравнение к стандартному (для
этого раздела) виду:
> eq:=x^2-2-ln(x+5)=0;
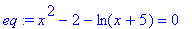
Теперь построим график левой части
уравнения:
> plot(lhs(eq),x=-10..10);
![[Maple Plot]](images/462.gif)
По всей видимости, существует два корня.
Один примерно равен -2, а другой, похоже, 2.
Применим команду fsolve , ограничив
диапазон поиска:
> x[1]:=fsolve(eq,x=-5..0);
![x[1] := -1.780253527](images/463.gif)
> x[2]:=fsolve(eq,x=1..3);
![x[2] := 1.985924818](images/464.gif)
Непосредственной подстановкой проверим
корни:
> evalf(subs(x=x[1],eq));
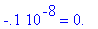
> evalf(subs(x=x[2],eq));
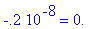
Обратите внимание: в обоих случаях
истинного равенства нет . С учётом ошибок при
округлении, разумное расхождение вполне
допустимо .
Убедитесь в отсутствии других корней.
Ответ обоснуйте.
Графики функций 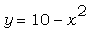 и и 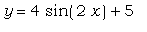 дважды пересекаются
на отрезке [-5;5]. дважды пересекаются
на отрезке [-5;5].
а). Постройте в одной системе координат
графики обеих функций и при помощи мыши найдите
координаты точек пересечения.
b). Составьте уравнение, корнями которого
являются абсциссы точек пересечения графиков.
c). Используйте команду fsolve для
решения этого уравнения.
d). Используйте результаты из пункта с)
для оценки ординат точек пересечения графиков.
e). У Вас не создалось впечатление, что
линии могут пересекаться и в третьей точке с
координатами (1;9)? Используйте fsolve и
графические возможности Maple, чтобы убедиться в
противном.
Учебная площадка 4.4
>
>
>
>
>
>
>
>
Ответ 4.4
a)
> y1:=10-x^2;
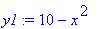
> y2:=4*sin(2*x)+5;
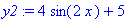
Теперь построим графики функций:
> plot([y1,y2],x=-5..5);
![[Maple Plot]](images/471.gif)
Приближенные координаты точек
пересечения: (-1.8, 6.6) и ( 2.75, 2) .
b) Составим уравнение:
> eq:= y1=y2;
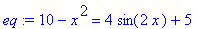
с) Команда fsolve поможет найти
соответствующие корни:
> x1:=fsolve(y1=y2,x=-4..0);
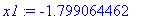
> x2:=fsolve(y1=y2,x=0..4);
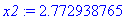
d) Используем команду subs для
определения соответствующих ординат точек
пересечения:
> y[1]:=subs(x=x1,y1);
![y[1] := 6.763367062](images/475.gif)
> y[2]:=subs(x=x2,y1);
![y[2] := 2.310810606](images/476.gif)
Общие точки графиков: (-1.800,6.763) и (2.773,2.311) .
e) Графически исследуем окрестность
точки х = 1:
> plot([y1,y2],x=.5..1.5);
![[Maple Plot]](images/477.gif)
Команда fsolve на этот раз позволит
доказать отсутствие корней вблизи точки х = 1 :
> fsolve(y1=y2,x=.5..1.5);
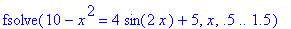
* Solving Literal Equations *
Во многих случаях Maple находит решение
уравнения в общем (символьном) виде. Речь идёт об
уравнении (а не системы!), содержащем несколько
переменных. Решение состоит в том, что какая-то из
переменных выражается через остальные.
Пусть необходимо решить уравнение 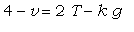 относительно переменной g . По привычке,
используем команду solve . И она оправдывает
наши надежды:
относительно переменной g . По привычке,
используем команду solve . И она оправдывает
наши надежды:
> solve(4-v=2*T-k*g,g);
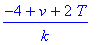
А так решение можно оформить в привычном
виде:
> g=solve(4-v=2*T-k*g,g);
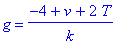
Решить последнее уравнение
относительно других переменных: T, k и v.
Учебная площадка 4.4
>
>
>
>
>
Ответ 4.4
> T=solve(4-v=2*T-k*g,T);
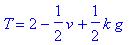
> k=solve(4-v=2*T-k*g,k);
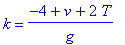
> v=solve(4-v=2*T-k*g,v);
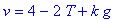
Решить уравнение 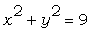 относительно у .
Присвоить последовательности корней имя S. Как
связаны корни S[1] и S[2] ? относительно у .
Присвоить последовательности корней имя S. Как
связаны корни S[1] и S[2] ?
Учебная площадка 4.5
>
>
>
>
>
Ответ 4.5
> S:=solve(x^2+y^2=25,y);

> S[1];
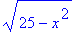
> S[2];

Корни отличаются только знаком.
* Solving a Linear System of Equations using the solve command
*
Пожалуйста, перед работой с новым
материалом выполните следующие две командные
строки:
> restart:
> with(plots):
Warning, the name changecoords has been redefined
Команда solve используется и для
решения системы из m линейных уравнений с n
неизвестными. Для краткости , в таких случаях
будем говорить: " линейная система m на n
".
Пример 01
Решить систему 2 на 2:
![PIECEWISE([``, 3*x+2*y = 3],[``, x-y = -4])](images/489.gif)
Вот как можно ввести систему уравнений в
привычном для математика виде, используя команду
piecewise :
> piecewise(3*x+2*y=3,``,x-y=-4,``);
![PIECEWISE([``, 3*x+2*y = 3],[``, x-y = -4])](images/490.gif)
Но для решения системы следует
применять команду solve :
> solve({3*x+2*y=3,x-y=-4});
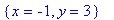
Можно предложить и графический вариант
решения. Легко получить единственную точку
пересечения прямых, соответствующих линейным
уравнениям. Координаты этой точки: (-1;3).
Если графики строить самым примитивным
способом, то придётся решить каждое из уравнений
относительно переменной y:
> y1:=solve(3*x+2*y=3,y);
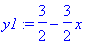
> y2:=solve(x-y=-4,y);
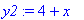
Предложим Maple изобразить в одной системе
координат комбинацию фигур. Фигуре из двух
пересекающихся прямых присвоим имя " крест
". Команду, выводящую на экран точку-решение,
назовём " точка ":
> крест:=plot([y1,y2],x=-5..5):
> точка:=plot([[-1,3]],style=point,color=blue,symbol=circle):
> display([крест,точка]);
![[Maple Plot]](images/494.gif)
Пример 02
А вот пример решения системы 3 на 3
относительно переменных x, y, и z .
Решить систему 3 на 3: ![PIECEWISE([``, x+y+z = 1],[``, 3*x+y = 3],[``, x-2*...](images/495.gif) , которую можно " нарисовать "
так: , которую можно " нарисовать "
так:
> piecewise(x+y+z=1,``,3*x+y=3,``,x-2*y-z=0,``);
![PIECEWISE([``, x+y+z = 1],[``, 3*x+y = 3],[``, x-2*...](images/496.gif)
Решать же следует так:
> solve({x+y+z=1, 3*x+y=3, x-2*y-z=0});
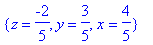
" Нарисовать " и решить систему
уравнений ![PIECEWISE([``, 4*x+3*y = 12],[``, 5*x-7*y = 35])](images/498.gif) . .
Решение проверить непосредственной
подстановкой в уравнения полученной пары чисел.
Учебная площадка 4.6
>
>
>
>
>
>
Ответ 4.6
> piecewise(4*x+3*y=12,``,5*x-7*y=35,``);
![PIECEWISE([``, 4*x+3*y = 12],[``, 5*x-7*y = 35])](images/499.gif)
> eqs:={4*x+3*y=12, 5*x-7*y=35};
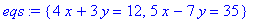
> XY:=solve(eqs);
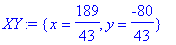
> subs(x=189/43,y=-80/43,eqs);
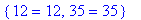
* Linear Systems with an Infinite Number of Solutions ( Optional )
*
Если число переменных в системе
линейных уравнений превышает число самих
уравнений, то говорят о поисках " общего
решения ".
Рассмотрим эту ситуацию на конкретном
примере.
Пример 01
Решим систему ![PIECEWISE([``, x+y+z = 1],[``, 3*x+y = 3])](images/4103.gif) : :
> sols:=solve({x+y+z=1, 3*x+y=3});
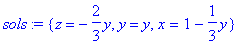
Итак, решением не будет единственная
тройка чисел ! Вместо этого, Maple выводит " общее
решение ": конструкция " х = х "
сообщает, какая неизвестная выбрана в качестве
" свободной ", а остальные
неизвестные выражаются через неё. Переменная х
может принимать любое действительное значение,
например, ![x[0]](images/4105.gif) . Тогда тройка чисел . Тогда тройка чисел ![`(`*x[0], 3-3*x[0], -2+2*x[0]*`)`](images/4106.gif) называется " частным решением ".
Таких троек - бесконечное число.
называется " частным решением ".
Таких троек - бесконечное число.
Например, пусть х = 4 :
> subs(x=4,sols);
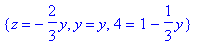
Получили одно из частных решений: х = 4 , y =
- 9 , z = 6 . Проверку можно выполнить даже устно.
"Добудем" ещё одно частное решение:
> subs(x=2,sols);
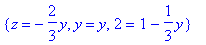
Найти общее решение системы ![PIECEWISE([``, x+2*y+z = 2],[``, 3*x+y = 1])](images/4109.gif) и не менее 3
частных. и не менее 3
частных.
Учебная площадка 4.7
>
>
>
>
>
Ответ 4.7
> piecewise(x+2*y+z=2,``,3*x+y=1,``);
![PIECEWISE([``, x+2*y+z = 2],[``, 3*x+y = 1])](images/4110.gif)
> eqs:={ x+2*y+z=2 , 3*x+y=1 };
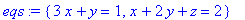
> sol:=solve(eqs);
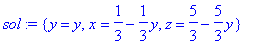
Получим частные решения:
> subs(x=1,sol);
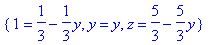
> subs(x=2,sol);
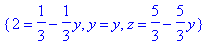
> subs(x=3,sol);
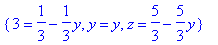
> subs(x=4,sol);
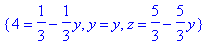
  
|

