| © 2000
Seattle Central Community College
публикуется с разрешения |
![[Maple OLE 2.0 Object]](../0/images/01.gif) ![[Maple OLE 2.0 Object]](../0/images/02.gif) |
 (31 Кб,
Maple) (31 Кб,
Maple)
 
В этом разделе Вы научитесь применять
Maple при проведении стандартных численных
расчётов. Уникальная способность Maple производить
точные вычисления (наряду с приближенными)
обеспечивает Вам дополнительные возможности при
решении вычислительных задач.
01.01. Точная Арифметика с Maple
01.02. Приближенные
Вычисления При Помощи Команды evalf
Упражнение 1.1
Упражнение 1.2
Упражнение 1.3
Упражнение 1.4
01.03. Работа С Переменными
* Doing Exact Arithmetic with Maple *
Использование Maple при проведении
численных расчётов выглядит довольно
естественно. Следует только ввести число и
завершить ввод командной строки символом "
; " ( точка с запятой ). Нажатие клавиши [ Enter
] при условии, что курсор размещен именно в этой
командной строке, приведёт к тому, что вслед за
командой в центре экрана появится результат,
набранный синим шрифтом .
Пример 01
Введём представленными ниже командными
строками простейшие вычислительные операции.
Щёлкнув где-нибудь на красном поле строки и нажав
клавишу [ Enter ] , получите результат.
> 2+4;
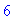
> 12*34567890;
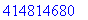
Каждая командная строка - "живая"
, т.е. её содержимое может быть подкорректировано
в любой момент.
Замените цифру " 4 " в первой
строке на " 8 " и нажмите [ Enter ] .
Отметьте для себя, как мгновенно на
экране обновляется синяя строка результата.
Пример 02
В качестве следующего примера вычислим 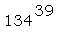 . .
> 134^39; 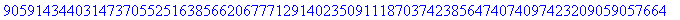
В отличие от самого мощного
микрокалькулятора, Maple (без дополнительных
программных ухищрений) мгновенно выдаёт точный
результат, все 83 значащие цифры!
Пример 03
Ещё одно достоинство Maple - он может точно
выполнять действия с обыкновенными дробями без
их обязательной конвертации в десятичную форму:
> 3/5 + 5/9 + 7/12;
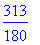
Пример 04
При вводе арифметических квадратных
корней используйте команду sqrt :
> sqrt(24);
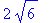
Заметьте, что Maple автоматически упрощает
иррациональность: вместо 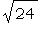 выводит выводит 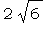 . .
В следующем параграфе Вы познакомитесь
с тем, как получить десятичное приближение этого
числа.
Пример 05
В Maple встроены фундаментальные
математические константы. Например, чтобы ввести
число 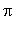 ,
следует набрать с клавиатуры Pi . Вы уже
заметили, что при вводе произведения множители
следует обязательно разделять символом " *
" ? ,
следует набрать с клавиатуры Pi . Вы уже
заметили, что при вводе произведения множители
следует обязательно разделять символом " *
" ?
> 4*(3+Pi);
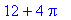
И вновь Maple выводит точное
иррациональное число, а не его приближенную
десятичную форму.
Пример 06
В отличие от Вашего калькулятора, Maple при
малейшей возможности выводит точные значения
функций, например, тригонометрических:
> sin(5*Pi/3);
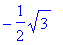
> sec(Pi/4);
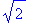
Чтобы найти значение арксинуса числа х
, используйте функцию arcsin(х) :
> arcsin(-1);
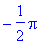
Если Вы требуете от Maple вычислить
значение функции в не принадлежащей её области
определения точке, то получите сообщение об
ошибке:
> tan(Pi/2);
Error, (in tan) numeric exception: division by zero
Пример 07
Чтобы ввести в Maple экспоненциальную
функцию, следует набрать:
> exp(x);
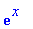
Чтобы ввести само число е - основание
натуральных логарифмов, наберите
> exp(1);

Пример 08
Чтобы ввести в Maple абсолютное значение
переменной х , используйте команду abs(x)
.
> abs(x);
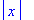
> abs(-3);
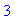
> abs(exp(1)-Pi);
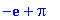
Заметьте, что Maple в последнем примере
вновь отдаёт предпочтение точному числу 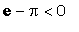 , намекая,
при этом, что оно - отрицательное ! , намекая,
при этом, что оно - отрицательное !
Пример 09
Maple обладает многими специальными
командами для работы с числами. Вы должны их
изучить, т.к. они используются практически во
всех разделах математики. Приведём пока лишь
один пример такой команды. Если Вы желаете
разложить целое число n на простые
множители, то используйте для этого Maple-команду ifactor(n)
. Не стесняйтесь экспериментировать, вводя самые
фантастические целые (и не только!) числа.
> ifactor(31722722304);
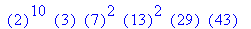
Пример 10
В дальнейшем, Вам неоднократно придётся
сталкиваться с необходимостью ввода сразу
нескольких команд в одной линии. В Maple такая
возможность предусмотрена. Если Вы при этом
желаете вывести на экран результаты всех команд,
то ввод каждой из них нужно завершать
символом " ; " . Если Вы после этого
нажмёте [ Enter ] , результаты выполнения команд
будут выведены в виде упорядоченного столбца, в
строгом соответствии с очередностью ввода
команд.
> sin(Pi/3); cos(Pi/3); tan(Pi/3);
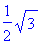
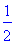
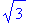
Пример 11
Чтобы вычислить и вывести на дисплей
последовательность чисел, используйте команду seq
. Ниже показывается, как вычислить квадраты
первых 100 натуральных чисел:
> seq(k^2,k=1..100);
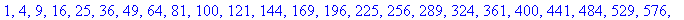
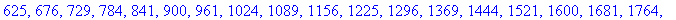
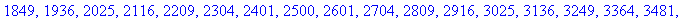
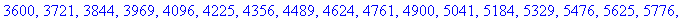
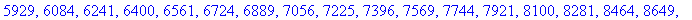
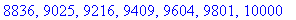
* Numerical Approximations using the evalf command
*
Напомним, что в предыдущем параграфе мы
просили Maple сложить три обыкновенные дроби.
Результат был выведен также в виде обыкновенной
дроби. Такой тип точных арифметических
вычислений необычайно важен, но иногда
предпочтительнее получить результат в
десятичной (как правило - приближенной) форме.
Нашим запросам в таких случаях отвечает команда evalf.
Пример 01
Сравните результаты двух следующих
командных строк:
> 3/5+5/9+7/12;
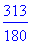
> evalf(3/5+5/9+7/12);
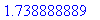
Пример 02
Своевременное присвоение имени
результату вычислений может в дальнейшем
заметно облегчить Вашу работу. Чтобы присвоить
имя k какому-то числу или функции K ,
используется оператор присваивания " :=
", состоящий из двоеточия и знака равенства: k:=K;
. В следующей командной строке имя " k " мы
присвоим сумме обыкновенных дробей, а затем
найдём десятичную форму этой суммы:
> k:=3/5+5/9+7/12;
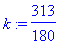
> evalf(k);
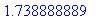
Важная черта Maple : система чётко
различает строчные и прописные буквы. Для Maple k
и K - совершенно разные символы.
> k;
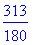
> K;
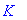
Кстати, в качестве имен, присваиваемых
числам и переменным, Вы можете использовать
слова и даже целые высказывания. В последнем
случае пропуски между словами следует заполнять
символом " _ " . ( В предыдущих версиях
Maple не допускалось использование кириллицы в
именах! ).
> Неуловимый_Джо:=2^5;
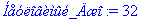
> sqrt(Неуловимый_Джо);
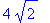
Пример 03
Если нам необходимо определенное
количество десятичных цифр в записи результата
(по умолчанию, Maple ограничивается десятью ), то
нужно после аргумента в команде evalf указать
необходимое число:
> w:=4*(3+Pi);
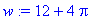
> evalf(w);
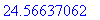
> evalf(w,4);
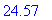
> evalf(w,45);
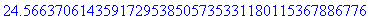
Пример 04
Если Вы введёте в командную строку хотя
бы одно число, в котором целая часть отделена от
дробной десятичной точкой , Maple автоматически
выведет результат в десятичной форме.
Сравните результаты двух командных
строк:
> sqrt(34);
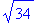
> sqrt(34.0);
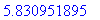
А вот другой пример:
> 4-1/3;
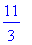
> 4.0-1/3;
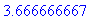
Пример 05
Вы можете применить команду evalf и к числовой
последовательности . Ниже вначале
генерируются точные значения квадратных корней
из первых 10 натуральных чисел, а затем, с помощью evalf
, находятся их приближенные десятичные значения:
> result:=seq(sqrt(k),k=1..10);
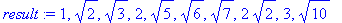
> evalf(result);
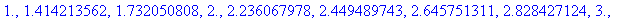
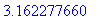
Maple-сокращения: Быстрый
вызов предыдущего результата
Из личного опыта Вы знаете, что
промежуточные результаты вычислений частенько
приходится не один раз переписывать. Работая с
Maple, Вы избавлены от необходимости в возможно
громоздком повторном наборе. При обращении к результату
последней операции , используйте символ
процента % :
> 3/5+5/9+7/12;
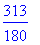
> evalf(%);
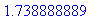
> Pi;
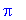
> evalf(%);
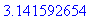
> %+5;
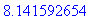
Другие подробности - см. в Упражнении
1.4.
Используя Maple, вычислить 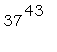 . .
Учебная площадка 1.1
>
>
>
>
Ответ 1.1
> 37^43;
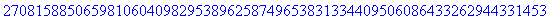
Вычислить 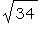 с точностью до 18 цифр. с точностью до 18 цифр.
Учебная площадка 1.2
>
>
>
Ответ 1.2
> m:=sqrt(34);
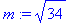
> evalf(m,18);
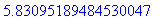
Получить численное приближение для 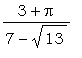 . .
Учебная площадка 1.3
>
>
>
Ответ 1.3
> answer:=(3+Pi)/(7-sqrt(13));
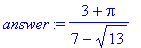
> evalf(answer);
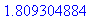
Символ процента % очень удобен для
сокращения вычислительного процесса. Однако,
можно получить и неожиданные (на первый взгляд)
результаты. Например, прокомментируйте
приведенные ниже три командные строки. На Ваш
взгляд: что должно быть выведено на экран?
> 4+Pi;
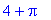
> evalf(%);
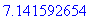
> %+10;
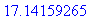
А теперь вновь выполните последнюю
команду (т.е. %+10; ). Заметьте, что теперь уже
будет выведено 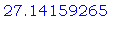 вместо вместо 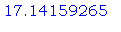 . Постарайтесь найти
этому объяснение. . Постарайтесь найти
этому объяснение.
Учебная площадка 1.4
>
>
Ответ 1.4
Символ % эквивалентен последнему
полученному результату. Повторно выполняя
команду %+10; , Maple прибавляет 10 к 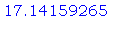 . Для упрощения
логики вычислений советуем почаще выполнять
операцию присваивания числам собственных имен: . Для упрощения
логики вычислений советуем почаще выполнять
операцию присваивания числам собственных имен:
> a:=4+Pi;
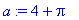
> b:=evalf(a);
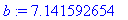
> b+10;
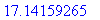
* Clearing Variables *
Достаточно Вам однажды определить
переменную, - и Maple будет помнить её значение на
протяжении всей Вашей рабочей сессии на
компьютере. Если Вам понадобилось
переопределить переменную - просто выполните
новую операцию присваивания.
Например, в каждой из приведенных ниже
строк в преобразованиях участвует переменная h
.( Замечание : для слежения за текущим
значением переменной h не забывайте
заканчивать ввод символом " точка с запятой
", а не " двоеточие ".)
> h;
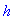
> h:=56;
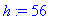
> h;
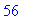
> h:=sqrt(Pi);
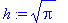
> h;

Иногда возникает желание
"очистить" переменную в памяти для того,
чтобы её имя впоследствии использовать в иных
целях.
Например, присвоим переменной х значение
65 :
> x:=65;
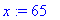
Теперь предположим, что мы, начиная
решение другой задачи, желаем присвоить имя w
квадратному трёхчлену 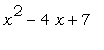 . Если без проволочек
выполнить указанную операцию присваивания, Maple
не задумываясь вместо переменной х подставит её
численное значение: . Если без проволочек
выполнить указанную операцию присваивания, Maple
не задумываясь вместо переменной х подставит её
численное значение:
> w:=x^2-4*x+7;
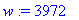
Чтобы переменная w предстала именно
в алгебраической форме, мы должны "очистить"
аргумент х от присвоенного ранее значения. На
практике это означает подчистку внутренней
памяти Maple. Это можно осуществить посредством
операции x:='x'; . ( Не путайте только одинарные
и двойные кавычки! )
Чтобы увидеть, как это работает,
выполните приведенные ниже командные строки:
> x:='x';
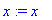
> w:=x^2-4*x+7;
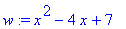
* Одновременная очистка всех переменных:
команда restart *
Команда restart полностью очищает
внутреннюю память Maple от всех определений,
которые Вы совершили в процессе работы.
Фактически, применение команды restart
открывает новую Maple-сессию. Если Вы приступаете к
решению совершенно новой задачи, советуем
использовать restart для полной гарантии того,
что предыдущие преобразования и вычисления не
повлияют на её решение.
Выполнив первую из предложенных ниже
командных линий, постарайтесь предсказать
результат выполнения второй строки:
> p:=4;
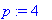
> p; x; h;
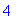
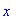

Конечно, Вы видете, что переменной р
присвоено значение " 4 ", а переменная х
была очищена от своего предыдущего числового
значения. Но очень вероятно, что Вы уже подзабыли,
что переменной h было присвоено значение 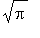 . Вот
почему так соблазнительна идея частого
использования команды restart , чтобы в одно
мгновение очистить память Maple от "грязи"
.(Если Вы будете внимательно прорабатывать
материал нашей обучающей программы, то обратите
внимание: большинство разделов начинается
именно командой restart ) . . Вот
почему так соблазнительна идея частого
использования команды restart , чтобы в одно
мгновение очистить память Maple от "грязи"
.(Если Вы будете внимательно прорабатывать
материал нашей обучающей программы, то обратите
внимание: большинство разделов начинается
именно командой restart ) .
> restart;
> p; x; h;
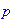
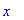
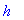
  
|

