| © 2000
Seattle Central Community College
публикуется с разрешения |
![[Maple OLE 2.0 Object]](../0/images/01.gif) ![[Maple OLE 2.0 Object]](../0/images/02.gif) |
 (38 Кб,
Maple) (38 Кб,
Maple)
 
В этом разделе Вы научитесь определять
функции в Maple, находить их значения. Кроме того, Вы
сможете развить навыки решения уравнений и
построения графиков.
05. 01 Определение и удаление
функций в Maple
Упражнение 5.1
05. 02 Вычисление значений
функции
Упражнение 5.2
05. 03 Решение функциональных
уравнений
05. 04 Построение графиков
функций
Упражнение 5.3
Упражнение 5.4
Упражнение 5.5
* Defining and Clearing a Function in Maple *
В Maple для определения функции и её
выделения на фоне обычных выражений
используется специальная форма записи.
Например, функция f(x) = 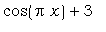 определяется так: определяется так:
> f:=x->cos(Pi*x)+3;
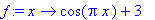
"Прочитаем": величина х
"переводится" в выражение 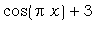 , которому
присваивается имя f ( это соответствует духу
определения функции f(x) ). Кроме известного Вам
оператора присваивания := , в этой конструкции
используются символы " минус " и " больше
", образующие " стрелку " -> . , которому
присваивается имя f ( это соответствует духу
определения функции f(x) ). Кроме известного Вам
оператора присваивания := , в этой конструкции
используются символы " минус " и " больше
", образующие " стрелку " -> .
Традиционная форма записи такой
функции: 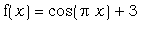 . .
Сравним формы, которые используются в
Maple для определения функции и аналогичного выражения
:
> y:=(x + 2)/(x^3 + 5*x + 2);
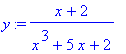
> f:=x->(x + 2)/(x^3 + 5*x + 2);
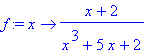
Конечно, и формы вывода на дисплей также
разнятся. Наличие стрелки - важнейший
отличительный знак функции в Maple .
Определите функцию h(x) = 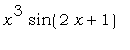 . .
Учебная площадка 5.1
>
>
>
Ответ 5.1
> h:= x-> x^3*sin(2*x+1);
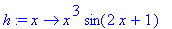
Если Вы единожды определили функцию, то
Maple это запомнит до окончания рабочей сессии.
Если Вы вдруг захотите переопределить функцию
f(x), например, на ln(cos 5x) , то просто напечатайте:
> f:=x->ln(cos(5*x));
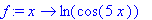
Можно вывести текущий вид функции f(x):
> f(x);
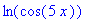
Можно избавить переменную f от её
функциональных обязанностей командой:
> f:='f';
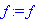
> f(x);
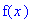
Напомним, что Maple обладает прекрасной
способностью очищать свою память по команде restart
. При этом все введенные Вами функции будут
стерты.
* Evaluating a Function *
Если Вы уже определили функцию, то
можете в любой момент и в любом месте
Maple-документа находить как численные, так и
символьные её значения. Во избежание
недоразумений, перед вводом новой функции,
избавьте от возможного прошлого её имя:
> f:='f';
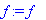
> f:=x->3*x+x^2;
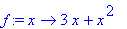
> f(-1);
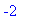
> f(2+sqrt(5));
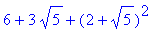
> evalf(f(2+sqrt(5)));
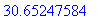
> f(x+4);
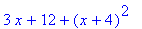
> simplify(%);
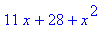
> (f(x+h)-f(x))/h;
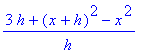
> simplify(%);
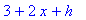
Если определено несколько функций, то
легко из них создать композицию ( сложную
функцию ):
> g:=x->cos(x)+1;
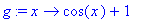
> f(g(Pi/3));
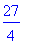
> j:=x->g(f(x));
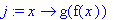
> j(x);
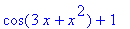
Определить функцию 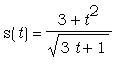 , а затем
найдите s(2), s(t-3) и s(t) - s(3) и результаты упростите.
Не забудьте о стрелках! , а затем
найдите s(2), s(t-3) и s(t) - s(3) и результаты упростите.
Не забудьте о стрелках!
Учебная площадка 5.2
>
>
>
>
>
>
>
>
>
>
Ответ 5.2
> s:= t-> (3 + t^2)/(sqrt(3*t+1));
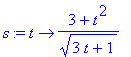
> s(2);
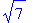
> s(t - 3);
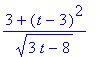
> simplify (%);
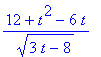
> s(t) - s(3);
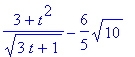
> simplify(%);
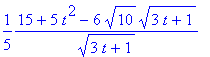
Заметьте, что если Вы определили
указанным образом функцию, уже нет необходимости
использовать команду subs для нахождения
значений функции, как в случае выражений.
* Solving Equations involving Functions *
Заранее определив функцию, Вы можете
составить и решить ( точно или приближенно )
содержащее её уравнение.
> g:='g';
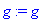
> g:=t->t^3-6*t^2+6*t+8;
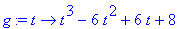
> solve(g(t)=0,t);
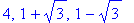
> fsolve(g(t)=0,t);
* Graphing a Function *
Для построения графиков функций
используется всё та же команда plot .
> h:='h'; y:='y'; x:='x';
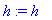
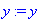
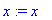
> h:=x->x*exp(-x);
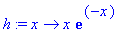
> plot(h(x),x=-1..4,y=-2..1);
![[Maple Plot]](images/543.gif)
Как и в случае выражений, в одной системе
координат можно построить графики сразу
нескольких функций.
Определим функцию 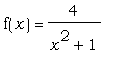 и построим
одновременно графики функций и построим
одновременно графики функций 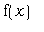 , , 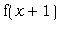 , , 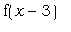 и и 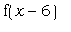 . Кривые получаются друг из
друга параллельным переносом. Попробуйте
установить соответствие между функциями и их
графиками. . Кривые получаются друг из
друга параллельным переносом. Попробуйте
установить соответствие между функциями и их
графиками.
> f:=x->2/(x^2+1);
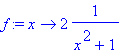
> plot([f(x),f(x+1),f(x-3),f(x-6)],x=-5..10,y=-1..3);
![[Maple Plot]](images/550.gif)
Определите функцию 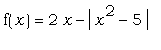 , а затем: , а затем:
a) Найдите значение f(6.5).
b) Найдите и упростите значение f(z-4), где z
- переменная.
c) Постройте график f(x)
d) Найдите все значения x, для которых f(x)=0.
Учебная площадка 5.3
>
>
>
>
>
>
>
>
>
>
Ответ 5.3
> f:=x->2*x-abs(x^2-5);
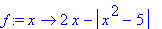
> f(6.5);
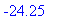
> simplify(f(z-4));
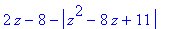
> plot(f(x),x);
![[Maple Plot]](images/555.gif)
> fsolve(f(x)=0,x=0..2);
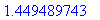
> fsolve(f(x)=0,x=3..4);
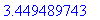
Определите функции 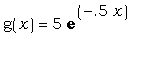 и и 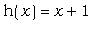 , а затем: , а затем:
a) В одной системе координат постройте
графики функций g(x) и h(x) .
Поэкспериментируйте с разными областями
определения и множествами значений функций.
b) Найдите координаты точки пересечения
графиков этих функций при помощи левой кнопки
мыши.
c) Воспользуйтесь fsolve для решения
уравнения g(x) = h(x) . Согласуется ли
результат с ответом на вопрос b) ?
Учебная площадка 5.4
>
>
>
>
>
>
>
>
>
>
>
>
Ответ 5.4
> g:=x->5*exp(-0.5*x);
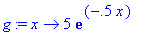
> h:=x->x+1;
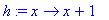
> plot([g(x),h(x)],x=-5..5,y=-20..20);
![[Maple Plot]](images/562.gif)
> plot([g(x),h(x)],x=1..2,y=1..4);
![[Maple Plot]](images/563.gif)
> xval:=fsolve(g(x)=h(x),x);
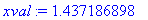
Корень уравнения g(x)=h(x) - абсцисса
точки пересечения графиков функций g(x) и h(x). Чтобы
найти соответствующую ординату, вычислите
значение функции g(x) или h(x) в этой точке.
> g(xval);
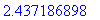
> h(xval);
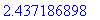
Определите функцию 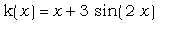 , а затем : , а затем :
a) Постройте её график на области
определения [-1,8] .
b) В этот график вставьте прямую y = 4.
Используя рисунок, определите число корней и их
приближенное значение уравнения k(x)=4 .
c) Графиком какой одной функции можно
было бы обойтись для отыскания указанных в b)
корней?
d) Воспользуйтесь Maple-команду fsolve для
нахождения приближенного решения уравнения k(x)=4.
Учебная площадка 5.5
>
>
>
>
>
>
>
>
Ответ 5.5
а)
> k:=x->x+3*sin(2*x);
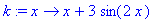
> plot(k(x),x=-1..8);
![[Maple Plot]](images/569.gif)
b)
> plot([k(x),4],x=-1..8);
![[Maple Plot]](images/570.gif)
с) Мы должны построить график функции k(x)
- 4 и определить абсциссы его точек пересечения с
осью Ох. Они соответствуют значениям х ,
найденным в b).
> plot(k(x)-4,x=-1..8);
![[Maple Plot]](images/571.gif)
Теперь найдём решение с помощью команды fsolve
:
> fsolve(k(x)=4,x=2 .. 3.5);
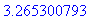
> fsolve(k(x)=4,x=3.5 .. 5);
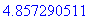
> fsolve(k(x)=4,x=5 .. 7);
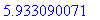
  
|

