Синтаксис:

Описание:

Функция Y = expm(A) является встроенной функцией интерпретатора системы MATLAB и вычисляет функцию e^A от матрицы A.

Функция Y = expm1(A) является M-файлом, который полностью соответствует встроенной функции expm(A). Он вычисляет функцию e^A, используя разложение Паде матрицы A [1].

Функция Y = expm2(A) вычисляет функцию e^A, используя разложение Тейлора матрицы A [2]. Этот метод имеет меньшую скорость сходимости по сравнению с разложением Паде.

Функция Y = expm3(A) вычисляет функцию e^A, используя спектральное разложение матрицы A:

             [R, D] = eig(A);
             Y = R * diag(exp(diag(D))) / R;,

которое, строго говоря, справедливо только для случая различных собственных значений.

Замечание:

Функцию матричной экспоненты expm(A) не следует путать с функцией exp(A), которая вычисляет экспоненту от каждого элемента массива A.

Пример:

Рассмотрим тестовую матрицу порядка n = 5 с дефектом 1, имеющую 5 кратных собственных значений, равных нулю [3].

Как следует из анализа полученных данных, функции expm(A) и expm1(A) дают совпадающие результаты, функция expm2(A) имеет погрешность в пределах ошибки округления, однако функция expm3(A) имеет ошибки в третьем знаке, что является следствием того, что исходная система меет кратные собственные значения.

Используя пакет программ JORD [4], можно выявить точную структуру формы Жордана матрицы A.

В данном случае это 1 клетка Жордана порядка 5, характеризующая простую однократную вырожденность.

Аналитическая функция f(J), где J - клетка Жордана, соответствующая собственному значению l, может быть вычислена следующим образом [4]:

          f(J) = .

В рассматриваемом случае матрица e^J равна

           EJ =

а матрица Y0 = e^A = R * e^J * R^-1 может быть вычислена так:

          Y0 = R * EJ / R.

Вычисленная матрица Y0 имеет вид

          Y0 =

Cчитая данное решение точным, оценим нормы невязок для предыдущих решений.

Из анализа следует, что функции expm1(A) и expm2(A) дают результаты с погрешностью в пределах ошибки округления, а функция expm3(A) имеет ту же погрешность.

Сопутствующие функции: EXP, FUNM, LOGM, SQRTM.

Ссылки:

1. Golub G. H., Van Loan. Matrix Computation. Oxford. John Hopkins University Press, 1983.

2. Moler C. B., Van Loan. Nineteen Dubious Ways to Compute the Exponential of a Matrix//SIAM Review, 1979. Vol. 20. P. 801-836.

3. Higham N. J. The Test Matrix Toolbox for MATLAB (version 3.0)//Numerical Analysis Report. Manchester, 1995. Vol. 276.

4. Потемкин В. Г. Пакет программ JORD. М.: МИФИ, 1995.
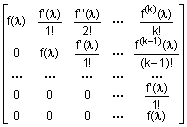