Синтаксис:

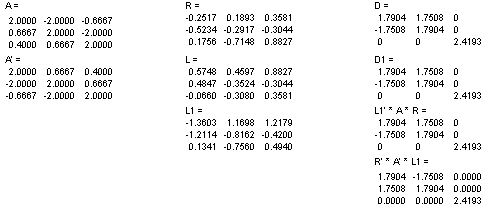
Описание:

Проблема собственных значений состоит в нахождении нетривиальных решений системы уравнений, которая может быть интерпретирована как алгебраический эквивалент системы обыкновенных дифференциальных уравнений в явной форме Коши:

           Ar = l r,

где A - квадратная матрица порядка n;
      r - вектор-столбец размера 1х n, называемый собственным вектором;
      l - скаляр, называемый собственным значением.

Функция d = eig(A) вычисляет собственные значения матрицы A.

Функция [R, D] = eig(A) вычисляет диагональную матрицу D собственных значений и матрицу R правых собственных векторов, удовлетворяющих соотношению A * R = R * D. Эти векторы нормированы так, что норма каждого из них равна единице.

Левые собственные векторы могут быть найдены следующим образом:
              [L, D] = eig(A’);

Матрицы собственных значений D для A и A’ содержат одни и те же собственные значения, хотя порядок их следования может быть различен. Матрица левых собственных векторов удовлетворяет соотношению A’ * L = L * D. Для согласования независимо найденных систем правых и левых собственных векторов систему левых векторов необходимо нормировать так, чтобы соблюдалось условие L * R = eye(n,n).

Функция [R, D] = cdf2rdf(R, D) преобразовывает комплексные выходы функции   eig в действительные, при этом комплексные собственные значения преобразовываются в блоки размера 2 х 2, а комплексная матрица правых собственных векторов R преобразовывается в действительную, столбцы которой, соответствующие действительным собственным значениям, сохраняются, а соответствующие комплексным - расщепляются на два: [Re(ri) Im(ri)].

Пример 1:

Рассмотрим матрицу порядка 3 с одним действительным и парой комплексно сопряженных собственных значений и выполним вычисления с использованием комплексных матриц.

Применяя функцию cdf2rdf, эти же вычисления можно реализовать, используя только действительные матрицы, что позволяет более экономно расходовать память.

Функция [R, D] = eig(A, ‘nobalance’) вычисляет собственные значения и собственные векторы без предварительного масштабирования матрицы. Обычно, масштабирование улучшает обусловленность матрицы, гарантируя большую точность вычислений. Однако когда матрица содержит очень малые по величине элементы, которые находятся в пределах ошибок округления, масштабирование может сделать их сравнимыми с другими элементами матрицы, что может привести к неправильным результатам.

Пример 2:

Рассмотрим матрицу порядка 4, которая содержит элементы, сравнимые с ошибками округления.

        B = ;

Как следует из этого примера, собственные значения в обоих случаях вычислены правильно, но нормы невязок различаются очень существенно, что свидетельствует о том, что собственные векторы в первом случае вычислены неверно.

Обобщенная проблема собственных значений состоит в нахождении нетривиальных решений системы уравнений

           Ar = l Br,

где A, B - квадратные матрицы порядка n;
      r - вектор-столбец размера 1 х n, называемый обобщенным собственным вектором;
      l - скаляр, называемый обобщенным собственным значением.

Вычисления с использованием комплексных матриц:

Вычисления с использованием только действительных матриц:

Если B - невырожденная матрица, то система может быть рассмотрена как алгебраический эквивалент системы обыкновенных дифференциальных уравнений в неявной форме Коши, а задача может быть сведена к обычной проблеме собственных значений

           B^-1Ar = l r.

В случае, когда B - вырожденная матрица, система уравнений представляет собой смешанную систему дифференциальных и алгебраических уравнений и для ее решения необходимо применять специальные методы.

Функция d = eig(A, B) вычисляет обобщенные собственные значения матрицы A.

Функция [R, D] = eig(A, B) вычисляет диагональную матрицу D обобщенных собственных значений и матрицу R правых обобщенных собственных векторов, удовлетворяющих соотношению A * R = B * R * D. Эти векторы нормированы так, что норма каждого из них равна единице.

Алгоритм:

Для действительных матриц функция eig(A) использует следующие модули пакета EISPACK [1-2]: balance, balbak, orthes, ortran и hqr2. Модули balance и balbak связаны с операциями масштабирования и восстановления; модуль orthes осуществляет приведение матрицы к форме Хессенберга посредством ортогональных подобных преобразований; модуль ortran запоминает все преобразования; модуль hqr2 вычисляет собственные значения и векторы матрицы в верхней форме Хессенберга с использованием QR-алгоритма Франсиса и Кублановской [3].

Функция eig(A, B) использует другие модули пакета EISPACK [1-2]: qzhes, qzit, qzval, и qzvec, основанные на QZ-алгоритме.

Для комплексных матриц функция eig(A) использует QZ-алгоритм, решая задачу в форме eig(A, eye(A)).

Диагностические сообщения:

Если в течение 30*n итераций собственные значения не найдены, выдается сообщение
          Solution will not converge.
          Решение не сходится.

Сопутствующие функции: BALANCE, HESS, QZ, SCHUR.

Ссылки:

1. Smith B. T., Boyle J. M., Dongarra J. J., Garbow B. S., Ikebe Y., Klema V., Moler C. B.. Matrix Eigensystem Routines - EISPACK//Guide. Lecture Notes in Computer Science. Berlin, 1976. Vol. 6.

2. Garbow B. S., Boyle J. M., Dongarra J. J., Moler C. B.. Matrix Eigensystem Routines - EISPACK Guide Extension//Lecture Notes in Computer Science. Berlin, 1977. Vol. 51.

3. Уилкинсон, Райнш. Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра: Пер. с англ. М.: Машиностроение, 1976. 390 с.

4. Moler C. B., Stewart G. W. An Algorithm for Generalized Matrix Eigenvalue Problems//SIAM J. Numer. Anal. 1973. N 2. Vol. 10.
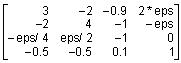