Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример
4 ~ Пример 5
Пример 1. Вычисление норм вектора и матрицы.
Даны вектор b =  и матрица A = и матрица A = 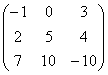 . Вычислить нормы вектора и
матрицы. . Вычислить нормы вектора и
матрицы.
Вычислим нормы вектора: 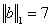 , , 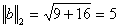 , , 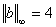 . .
Соответствующие нормы матрицы:
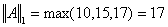 , , 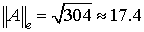 , , 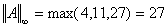 . .
Теоретическая справка
Вернуться на
страницу <Введение в вычислительную
математику. Примеры>

Пример 2. Вычисление норм матрицы.
Вернуться
на страницу <Введение в вычислительную
математику. Примеры>

Пример 3. Оценка числа обусловленности и эксперимент.
Вернуться
на страницу <Введение в вычислительную
математику. Примеры>

Пример 4.
Разложение матрицы A на множители.
A = 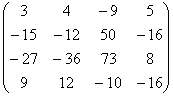
1-й шаг. Вычислим масштабирующие множители 1-го
шага
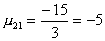 , , 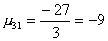 ,
, 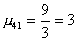 . .
и выполним преобразование матрицы: 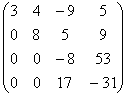
2-ой шаг. Вычислим масштабирующие множители 2-го
шага
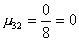 и и 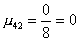 . .
2-ой шаг не изменяет матрицы. A2 = A1.
3-й шаг. Вычислим масштабирующие множители 3-го
шага
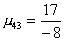 . .
и выполним преобразование матрицы: A3
= 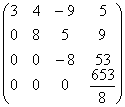
В результате получим матрицу U.
Таким образом, L = 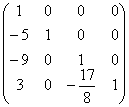 , U
= , U
= 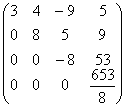 . .
Вернуться
на страницу <Введение в вычислительную
математику. Примеры>

Пример 5.
Решение системы с помощью LU - разложения матрицы.
Решим систему уравнений Ax = b с матрицей A,
рассмотренной в примере 4 и вектором 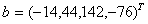 .
После разложения матрицы на множители, решение
системы сводится к последовательному решению
систем с треугольными матрицами: .
После разложения матрицы на множители, решение
системы сводится к последовательному решению
систем с треугольными матрицами: 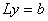 и и 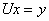 . .
Легко проверить, что решением 1-ой системы
является вектор 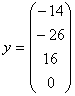 , ,
а решением 2-ой системы является вектор 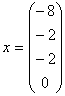 . .
Вернуться
на страницу <Введение в вычислительную
математику. Примеры>

|

