Пример 1 ~ Пример 2 ~ Пример 3
Пример 1. Найдем плотность вероятностей случайной
величины h = ex для
x , имеющей стандартное нормальное
распределение N(0, 1).
Распределение, полученное в результате,
называется логнормальным.
Пример 2. Найдем плотности вероятностей случайных
величин h = x 1 + x 2 и h = x
1 + x 1 = 2x 1,
где x 1 и x 2 —
независимые случайные величины со стандартными
нормальными распределениями.
Распределения случайных величин h
= x 1 + x 2 и
h = x 1 + x 1 = 2x 1
различны. В первом случае получено нормальное
распределение с параметрами a = 0, 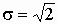 , а во втором —
нормальное распределение с параметрами a = 0, s = 2.
Вернуться на
страницу <Курс теории вероятностей. Примеры>
Пример 3. Пусть (x , h
) — дискретный случайный вектор с
распределением:
| |
1 |
2 |
3 |
4 |
| 0 |
0.01 |
0.02 |
0.03 |
0.04 |
| 1 |
0.1 |
0.1 |
0.2 |
0.4 |
| 2 |
0.05 |
0.01 |
0.01 |
0.03 |
Найдем распределение случайной величины z = x h .
Очевидно, что случайная величина z
= x h принимает
значения 0, 1, 2, 3, 4, 6, 8.
Вычислим соответствующие вероятности:
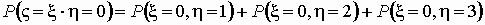
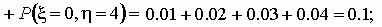
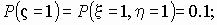
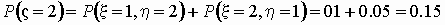 и
т.д.
В результате получим распределение случайной
величины  :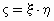
| z |
0 |
1 |
2 |
3 |
4 |
6 |
8 |
| p |
0.1 |
0.1 |
0.15 |
0.2 |
0.41 |
0.01 |
0.03 |
Вернуться на
страницу <Курс теории вероятностей. Примеры>
|
