Первый способ.

Определим функцию случайной величины h = exp(x)

Вычислим и определим обратную функцию для функции y = exp(x)

                    

Для того чтобы найти обратную функцию к функции y=f(x), введите f(x)-y, выделите x, выполните процедуру Variables - Solve в меню Symbolics и, используя полученное решение, определите обратную функцию finv(x)

Вычислим и определим производную обратной функции

        

Определим плотность распределения случайной величины x - плотность распределения стандартного нормального закона.

По формуле      

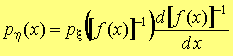
определим плотность распределения случайной величины h = f(x)

            

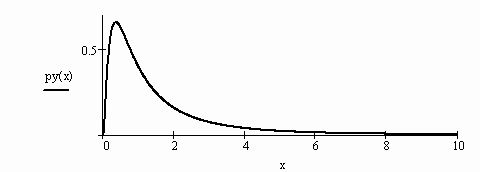
Такое распределение называется логнормальным

Построим график плотности распределения py(x) случайной величины h = f(x)

Второй способ.

Определим функцию случайной величины h = exp(x)

Вычислим и определим обратную функцию для функции y = exp(x)

                    

Вычислим и определим производную обратной функции

        

Определим плотность распределения случайной величины x - плотность распределения стандартного нормального закона.

                   

Определим плотность распределения случайной величины h = f(x) по формуле py(x)=px(f-1(x))(f-1(x))'

Для того чтобы выполнить в выражении для плотности распределения px(x) подстановку x<>finv(x), скопируйте в буфер выражение для finv(x), введите выражение для px(x), выделите в нем переменную x, выполните процедуру Variables - Substitute в меню Symbolics и, используя полученное решение, определите функцию py(x)

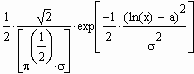
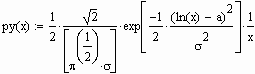          Такое распределение называется логнормальным.

Построим график плотности распределения py(x) случайной величины h = f(x)