Пример 1
~ Пример 2 ~ Пример 3
~ Пример 4 ~ Пример 5
Пример 1. Найти угол между векторами
Пусть в декартовой системе координат а={2,1,0},
b={3,-2,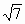 },
c={-4,-2,0}.
Найти угол между векторами },
c={-4,-2,0}.
Найти угол между векторами
а) a и b;
б) а и с.

Пример 2. Вычислить площадь параллелограмма, построенного на векторах a
и b.
Вычислить площадь параллелограмма, построенного на векторах a и b,
если a=p+2q, b=3p-2q, |p|=1, |q|=1/2,
φp,q= p/6.
Решение: Пусть Sa,b – искомая площадь.
[a,b] = [p+2q,3p-2q] = [p, 3p-2q]+2[q,
3p-2q] = 3[p,p]-2[p,q]+2·3[q,p]-2·2[q,q] =
= θ-2[p,q]+6[q,p]-θ = 2[q,p]+
6[q,p] = 8[q,p].
Sa,b = | [a,b] | =
| 8[q,p] | = 8·|q|·|p|·
sinφp,q = 8·1·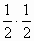 = 2. = 2.
Ответ: Sa,b = 2.

Пример 3. Проверка компланарности векторов
Компланарны ли векторы a={1,0,1}, b={0,2,-1}, c={3,1,0}?

Пример 4. Принадлежность 4 точек одной плоскости
Доказать, что точки А(1,2,-5), B(2,-1,-10), C(-1,3,0) и D(-4,-2,1) лежат в одной плоскости.

Пример 5. Вычислить объем тетраэдра и его высоту
Вычислить объём тетраэдра с вершинами в точках А1, А2,
А3, А4 и его высоту, опущенную из вершины А4 на
грань А1А2А3, если А1(1,2,0), А2(-1,2,1),
А3(-1,-1,-1), А4(0,1,3).

|

