Пример 1 ~ Пример 2 ~ Пример 3
Пример 1.
Вычислить интеграл 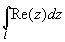 , где: , где:
а). l - прямая, соединяющая точки z1= 0
и z2 = 1+i;
б). l - ломаная ОВА, О(0,0), В(1,0),
А(1,1).
Решение.
а). Путь интегрирования l - прямая, соединяющая
точки z1=0 и z2 = 1+i.
Применяем к вычислению интеграла 1-й способ (формула
(1)). Подинтегральное выражение имеет вид
Re zdz = x(dx+idy) = xdx + ixdy.
Поэтому:
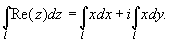
Уравнение отрезка прямой, соединяющей точки z1=0
и z2 = 1+i имеет вид
y = x, 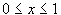 . .
Получаем:
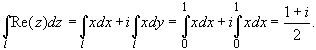
б). Путь интегрирования l -
ломаная ОВА, О(0,0), В(1,0), А(1,1).
Так как путь интегрирования состоит из двух
отрезков, записываем интеграл в виде суммы двух
интегралов:
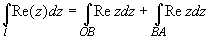
и каждый из этих двух интегралов вычисляем, как
выше.
Для отрезка ОВ имеем: y = 0, 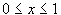 , ,
а для отрезка ВА: х = 1, 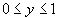 . .
Тогда:
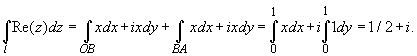
Заметим, что подинтегральная функция в
данном примере - функция не аналитическая,
поэтому интегралы по двум различным кривым,
соединящим две данные точки, могут иметь
различные значения, что и продемонстрировано в
этом примере.

Пример 2. Вычислить интеграл 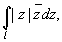
l - верхняя полуокружность |z| = 1, обход l
против часовой стрелки.
Подинтегральная функция здесь непрерывная, но
не аналитичная функция. Применим второй способ (формула
(2)), поскольку кривая l имеет простое
параметрическое представление:
z = eit, 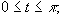
Тогда 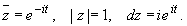
Подставляем в подинтегральное выражение имеем:
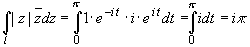

Пример 3.
Вычислить интеграл от аналитической
функции 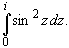
Применяем формулу (3), первообразную находим,
используя методы интегрирования
действительного анализа:
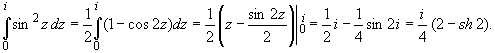

|

