Интеграл от
функций комплексного переменного ~ 1-й
способ вычисления интегралов ~ 2-й
способ вычисления интегралов ~ 3-й
способ вычисления интегралов
Интегралом от функции
комплексного переменного называется предел
последовательности интегральных сумм; функция
при этом определена на некоторой кривой l,
кривая предполагается гладкой или
кусочно-гладкой:
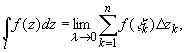
где 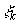 - точка, произвольно выбранная
на дуге - точка, произвольно выбранная
на дуге 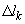 разбиения кривой, разбиения кривой,
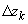 - приращение аргумента функции на этом
участке разбиения,
- приращение аргумента функции на этом
участке разбиения,
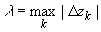 - шаг разбиения,
- шаг разбиения,
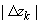 -
длина хорды, соединяющей концы дуги -
длина хорды, соединяющей концы дуги 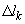 , ,
кривая l разбивается произвольным образом на n
частей 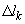 , k=1,2...n. , k=1,2...n.
На кривой выбрано направление, т.е. указаны
начальная и конечная точки.
В случае замкнутой кривой l = C
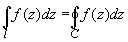
интегрирование происходит в положительном
направлении, т.е. в направлении обхода,
оставляющем слева конечную область,
ограниченную контуром С.
Существует несколько способов вычисления
интегралов в комплексной области.
1 способ. Интеграл
вычисляется сведением к криволинейным
интегралам от функций действительных переменных
- примененяются формулы:
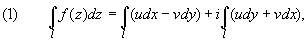
где f(z) = u + iv, u = Re f(z), v
= Im f(z).
ПРИМЕР 1. Вычисление интеграла.
2 способ. Интеграл
вычисляется сведением к определенному интегралу
(путь интегрирования l задается в
параметрической форме z = z(t)) -
применяется формула:
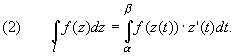
ПРИМЕР 2. Вычисление интеграла.
3 способ. Вычисление
интегралов от аналитической функции в
односвязных областях - примененяеется формула:
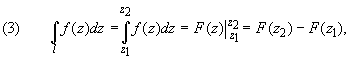
где F(z) - первообразная для f(z).
ПРИМЕР 3. Вычисление интеграла.

|

