Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример 4 ~ Пример 5 ~ Пример 6

Пример 1. Движение материальной точки массы m под действием внешних сил F описывается вторым законом Ньютона ma = F .
Пусть точка движется по оси 0x , тогда функция x = x(t) — абсцисса точки в момент времени t , удовлетворяет обыкновенному дифференциальному уравнению 2-го порядка mx'' = F(t, x, x').
Например, уравнение
x'' + w²x=0
— уравнение гармонического осциллятора, описывает периодические колебания материальной точки с периодом T=2p/w.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

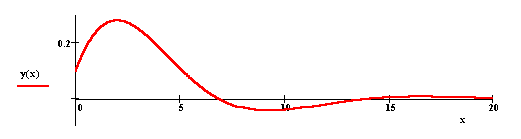
Пример 2. Изменение объема производства в некоторой замкнутой экономической системе описывает дифференциальное уравнение второго порядка
y'' +2|k|y' + w²y = 0.
В замкнутой экономической системе нет экспорта, импорта и притока капитала извне. Уравнение описывает поведение разности
y(x)=Y(x)-G/s
между объемом производства Y(x) и фиксированной величиной G/s отношения правительственных расходов к предельной склонности населения к сбережению.
Ниже приведен график решения уравнения при k=0.25, w²=0.25.
Колебания решения уравнения около нуля соответствуют периодам спада и подъема в экономике.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 3. Уравнение гармонического осциллятора
x'' + w²x = 0
описывает периодические колебания материальной точки с периодом T=2p/w². Легко проверить, что
x=С₁cos(wt)+С₂sin(wt) является решением уравнения гармонического осциллятора при любых значениях констант С₁ и С₂.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

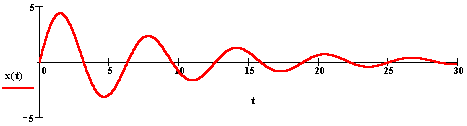
Пример 4.  Уравнение второго порядка
x'' + 2ax' + bx = 0
при a²<b описывает затухающие (ангармонические) колебания.
Ниже приведен график решения уравнения для a=0.1, b=1.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

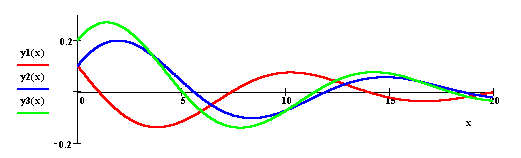
Пример 5. Изменение объема производства в некоторой замкнутой экономической системе описывает дифференциальное уравнение второго порядка
y'' +2|k|y' + w²y = 0.
В замкнутой экономической системе нет экспорта, импорта и притока капитала извне. Уравнение описывает поведение разности y(x)=Y(x)-G/s
между объемом производства Y(x) и фиксированной величиной G/s отношения правительственных расходов к предельной склонности населения к сбережению.
Ниже приведены графики решений уравнения при k=0.25, w²=0.25 при различных начальных условиях. Видно, что колебания решений около нуля — периоды спада и подъема в экономике — зависят от начального состояния системы.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 6. Решим методом Рунге-Кутте задачу Коши для дифференциального уравнения второго порядка
y'' + 16y = 3cos(4.1x), y(0)=0, y'(0)=0.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica