Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример 4 ~ Пример 5 ~ Пример 6~ Пример 7 ~ Пример 8

Пример 1. Поведение решений в окрестности устойчивого узла

Рассмотрим автономную систему

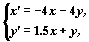
ее собственные значения l₁ = -1 и l₂ = -2 — отрицательные действительные числа. Следовательно, точка покоя (0, 0) — устойчивый узел.
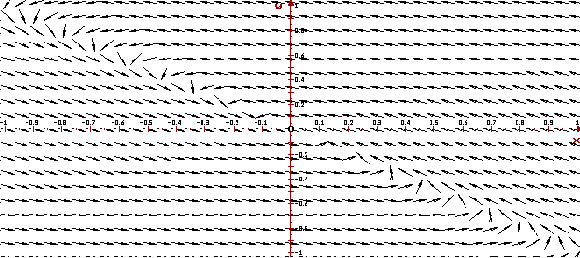
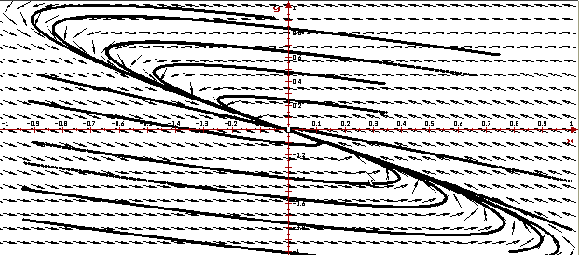
Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 2. Поведение решений в окрестности неустойчивого узла

Рассмотрим автономную систему

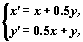
ее собственные значения l₁ = 1.5 и l₂ = 0.5 — положительные действительные числа. Следовательно, точка покоя (0, 0) — неустойчивый узел. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

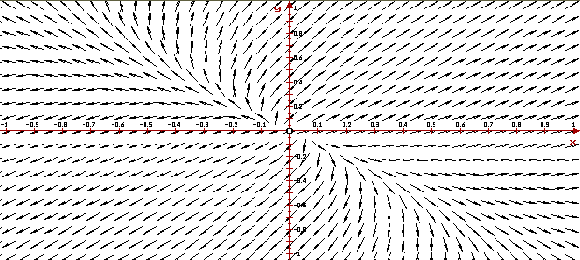
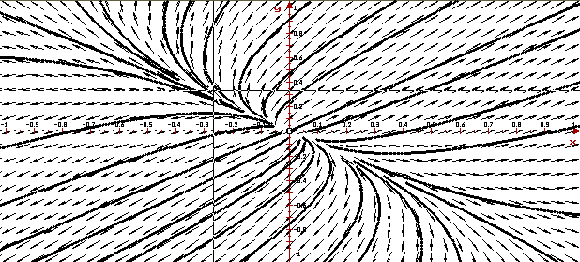
Пример 3. Поведение решений в окрестности седла

Рассмотрим автономную систему

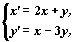
ее собственные значения
,
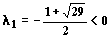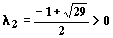
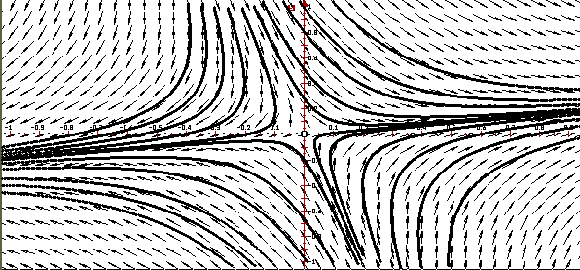
— действительные числа разных знаков. Следовательно, точка покоя (0, 0) — неустойчива, седло. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 4. Поведение решений в окрестности центра

Рассмотрим автономную систему

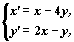
ее собственные значения 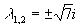— мнимые числа. Следовательно, точка покоя (0, 0) — центр, устойчивая, но не асимптотически устойчивая точка покоя. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

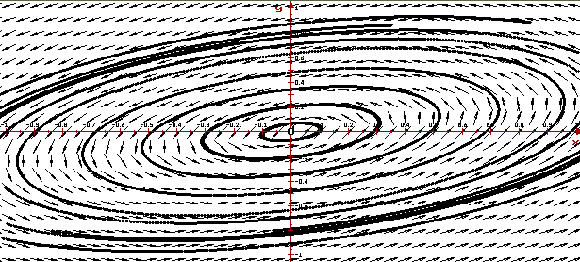
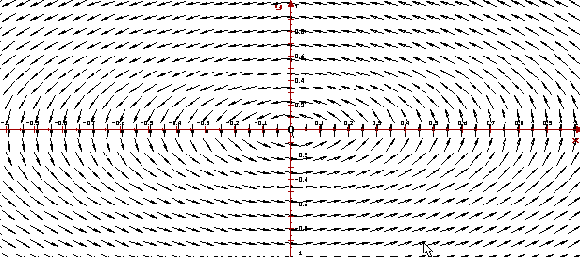
Пример 5. Поведение решений в окрестности устойчивого фокуса

Рассмотрим автономную систему

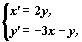
ее собственные значения 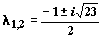— комплексные числа с отрицательными действительными частями. Следовательно, точка покоя (0, 0) — устойчивый фокус. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

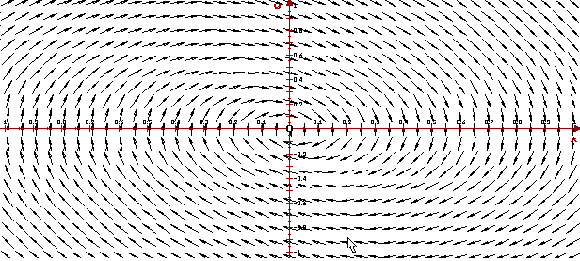
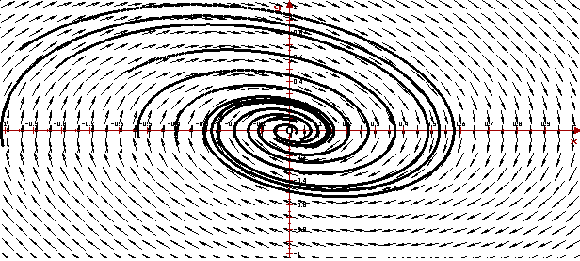
Пример 6. Поведение решений в окрестности неустойчивого фокуса

Рассмотрим автономную систему

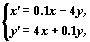
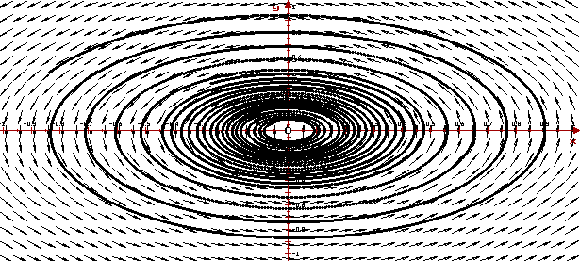
ее собственные значения l₁ = 0.1+4 i и l₂ = 0.1-4 i — комплексные числа с положительными действительными частями. Следовательно, точка покоя (0, 0) — неустойчивый фокус. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 7. Поведение решений в окрестности диакритического узла

Рассмотрим автономную систему

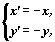
ее собственные значения l₁ = l₂ = -1 — одинаковые действительные числа. Следовательно, точка покоя (0, 0) — устойчивый диакритический узел. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 8. Автономная система с бесконечным множеством точек покоя

Рассмотрим автономную систему

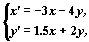
ее собственные значения l₁ = 0 и l₂ = 1. Следовательно система имеет бесконечное множество точек покоя, расположенных на прямиой 3x+4y=0. Ниже приведено изображение векторного поля системы и ее фазовый портрет, построенные программой ОДУ.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica