Метод вариации произвольных постоянных для уравнения второго порядка. Метод вариации произвольных постоянных для уравнений высших порядков ~ Алгоритм решения задачи Коши методом вариации призвольных постоянных ~ Алгоритм вычисления общего решения методом вариации произвольных постоянных

Доказано, что для линейного неоднородного дифференциального уравнения
y⁽ⁿ⁾ + a₁ y^(n-1) + ... + a_n-1 y' + a_n y = f(x)
при непрерывной правой части f(x), для любых начальных значений
x₀,  y₀,   y_0,1, ..., y_0,n-1
существует и единственно решение задачи Коши
y(x₀)=y₀, (y)'(x₀)=y_0,1 , ...,(y)^(n-1)(x₀)=y_0,n-1.

Решение задачи Коши для неоднородного дифференциального уравнения с постоянными коэффициентами можно найти методом вариации произвольных постоянных (методом Лагранжа), который состоит в следующем:
Записываем искомое решение задачи Коши для неоднородного уравнения  в виде
y(x)= c₁(x) y₁(x) +  c₂(x) y₂(x) + ... + c_n(x) y_n(x),
где  y₁(x),  y₂(x), ..., y_n(x)  — линейно независимые решения соответствующего однородного уравнения, и находим неизвестные функции
c₁(x) ,  c₂(x), ...,  c_n(x),
такие, чтобы функция y = y(x) удовлетворяла неоднородному уравнению и заданным начальным условиям.

Опишем алгоритм решения задачи Коши для уравнения второго порядка
y'' + a₁ y' + a₂ y = f(x), y(x₀)=y₀, (y)'(x₀)=y_0,1.
Будем искать решение задачи в виде
y(x)= c₁(x) y₁(x) +  c₂(x) y₂(x),
где  y₁(x),  y₂(x) — линейно независимые решения однородного уравнения
y'' + a₁ y' + a₂ y = 0.
Вычислим  y'(x), y''(x)  и подставим полученные выражения в уравнение.
Вычислим первую производную
y'(x)= (c₁'(x) y₁(x) +  c₂(x)' y₂(x)) + (c₁(x) y₁'(x) +  c₂(x) y₂'(x)),
положим
c₁'(x) y₁(x) +  c₂(x)' y₂(x)  = 0
и тогда
y'(x)= c₁(x) y₁'(x) +  c₂(x) y₂'(x),
y''(x)= (y'(x))'= (c₁(x) y₁'(x) +  c₂(x) y₂'(x))'=
=c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) + c₁(x) y₁''(x) +  c₂(x) y₂''(x).

Подставив y(x) и ее производные в уравнение, получим:
y'' + a₁ y' + a₂ y =
= c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) + c₁(x) y₁''(x) +  c₂(x) y₂''(x) +
+ a₁(c₁(x) y₁'(x)+c₂(x) y₂'(x)) + a₂(c₁(x) y₁(x)+c₂(x) y₂(x)) =
= c₁(x)( y₁''(x)+a₁ y₁'(x)+a₂ y₁(x)) + c₂(x)( y₂''(x)+a₁ y₂'(x)+a₂ y₂(x)) +
+ c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) = 0 + 0 + c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) = f(x),
при условии c₁'(x) y₁(x) +  c₂(x)' y₂(x)  = 0.

Тогда неизвестные функции c₁(x) и c₂(x) являются решениями системы линейных дифференциальных уравнений
c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) =  f(x),
c₁'(x) y₁(x) +  c₂(x)' y₂(x)  = 0
с известными y₁(x) и y₂(x).
Эта система легко разрешима относительно c₁(x) и c₂(x):
c₁'(x) =  f(x)y₂(x)/(y₁'(x)y₂(x)-y₁(x)y₂'(x)),
c₁'(x)= f(x)y₁(x)/(y₁(x)y₂'(x)-y₁'(x)y₂(x)).
Вычислив интегралы в правой части системы, получим

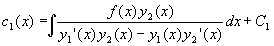
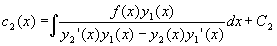
Произвольные константы C₁  и  C₂   определяются из начальных условий.

ПРИМЕР 1. Решение методом вариации задачи Коши для линейного  неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами.

Заметим, что разрешимость системы дифференциальных уравнений для
c₁'(x) и c₂'(x) и однозначная разрешимость системы начальных условий для произвольных констант C₁  и    C₂  гарантированы линейной независимостью  y₁(x) и y₂(x),
(y₁'(x)y₂(x)-y₁(x)y₂'(x))№0 для линейно независимых y₁(x) и y₂(x).

Для того чтобы решить задачу Коши для уравнения более высокого порядка действуем аналогично.
Решение задачи Коши ищем в виде
y(x)= c₁(x) y₁(x) +  c₂(x) y₂(x) + ... + c_n(x) y_n(x),
где  y₁(x),  y₂(x), ..., y_n(x)  — линейно независимые решения соответствующего однородного уравнения.
Неизвестные функции c₁(x) ,  c₂(x), ...,  c_n(x)
находим как решения линейной системы дифференциальных уравнений
c₁'(x) y₁(x) +  c₂(x)' y₂(x) + ... + c_n'(x) y_n(x) = 0
c₁'(x) y₁'(x) +  c₂'(x) y₂'(x) + ... + c_n'(x) y_n'(x) = 0,
c₁'(x) y₁''(x) +  c₂'(x) y₂''(x) + ... + c_n'(x) y_n''(x) = 0,
.................
c₁'(x) y₁^(n-1)(x) +  c₂'(x) y₂^(n-1)(x) + ... + c_n'(x) y_n^(n-1)(x) = f(x),
которая в силу линейной независимости y₁(x),   y₂(x), ..., y_n(x)   разрешима относительно c_i'(x).
Вычислив c_i(x) = F_i(x) + C_i находим произвольные постоянные C_i из начальных условий и тогда искомое решение уравнения имеет вид
y(x)= F₁(x) y₁(x) + F₂(x) y₂(x) +  ...+ F_n(x) y_n(x) + C₁y₁(x) + C₂ y₂(x) +...+ C_ny_n(x).

ПРИМЕР 2. Решение методом вариации произвольных постоянных задачи Коши для  линейного неоднородного дифференциального уравнения 3-го порядка с постоянными коэффициентами.

Таким образом, для того чтобы решить методом вариации произвольных постоянных решение задачи Коши для линейного неоднородного дифференциального уравнения  с постоянными коэффициентами следует:
записать характеристическое уравнение;
найти все корни характеристического уравнения l₁, l₂, ... , l_n;
найти фундаментальную систему решений y₁(x), y₂(x), ..., y_n(x));
представить искомое решение задачи Коши  в виде линейной комбинации 
y(x)= c₁(x)y₁(x) +  c₂(x)y₂(x) + ... + c_n(x)y_n(x),
с неизвестными функциями c₁(x), c₂(x), ...,  c_n(x);
составить и решить систему для c₁ (x), c₂(x), ...,  c_n(x);
подставить вычисленные c_i(x) = F_i(x) + C_i  в выражение для решения и записать для него начальные условия;
найти из начальных условий значения констант C_i и записать искомое решение.

ПРИМЕР 3. Решение методом вариации произвольных постоянных задачи Коши для линейного неоднородного дифференциального уравнения 4-го порядка с постоянными коэффициентами.

Для отыскания общего решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами следует
найти общее решение соответствующего однородного уравнения (записать характеристическое уравнение, найти все корни характеристического уравнения l₁, l₂, ... , l_n, записать фундаментальную систему решений y₁(x), y₂(x), ..., y_n(x));
найти методом вариации произвольных постоянных любое частное решение неоднородного уравнения y_ч(x);
записать выражение для общего решения
y(x)= c₁ y₁(x) +  c₂ y₂(x) + ... + c_n y_n(x) + y_ч(x).

ПРИМЕР 4. Общее решение для линейного неоднородного дифференциального уравнения 4-го порядка с постоянными коэффициентами.