Предел
суммы, произведения и частного функций ~ Неопределенности и их раскрытие ~ Использование эквивалентных
бесконечно малых ~ Правило
Лопиталя ~ Формула Тейлора
Предел суммы, произведения и частного
функций.
Пусть заданы две функции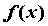 и и 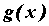 . Если существуют . Если существуют 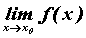 и и 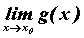 , то
существуют и пределы
суммы и произведения этих функций, а при , то
существуют и пределы
суммы и произведения этих функций, а при 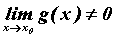 и
предел частного, причем и
предел частного, причем
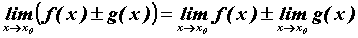 , ,
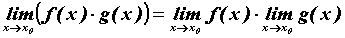 ,
,
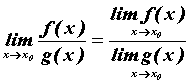 . .
Для правильного применения этих теорем очень
важно существование пределов каждой функции. Не
трудно доказать, что предел постоянной функции
равен этой постоянной, то есть 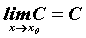 . Из
приведенных формул следует полезное
утверждение: . Из
приведенных формул следует полезное
утверждение:
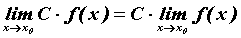 ,
то есть постоянный множитель можно выносить за
знак предела. Если сделать замену переменной ,
то есть постоянный множитель можно выносить за
знак предела. Если сделать замену переменной 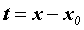 , то
вычисление предела при , то
вычисление предела при 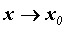 всегда можно свести к
вычислению предела при всегда можно свести к
вычислению предела при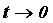 . Из определения непрерывной функции
следует, что ее предел совпадает со значением
функции в этой точке. Доказывают, что все
элементарные функции непрерывны в области
определения, поэтому, если функция определена, то
вычисление предела сводится к применению
указанных теорем и подстановке . Из определения непрерывной функции
следует, что ее предел совпадает со значением
функции в этой точке. Доказывают, что все
элементарные функции непрерывны в области
определения, поэтому, если функция определена, то
вычисление предела сводится к применению
указанных теорем и подстановке 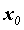 в выражение для
функции. в выражение для
функции.
ПРИМЕР 1 . Простейшие методы
вычисления пределов
Неопределенности и их раскрытие.
Существуют случаи, когда не применимы теоремы о
пределах суммы, произведения, частного, но предел
существует и может быть вычислен. Если 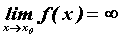 и и 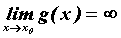 , то
может существовать , то
может существовать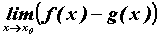 . В этом случае
говорят, что имеем неопределенность типа . В этом случае
говорят, что имеем неопределенность типа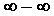 . Также
может существовать . Также
может существовать 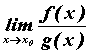 , в этом случае имеем
неопределенность типа , в этом случае имеем
неопределенность типа 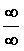 . Если . Если 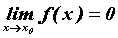 и и 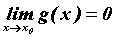 , то
может существовать , то
может существовать 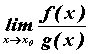 . В этом случае
говорят, что имеем неопределенность типа . В этом случае
говорят, что имеем неопределенность типа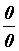 .
Если .
Если 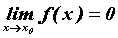 и и 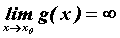 , то может
существовать , то может
существовать 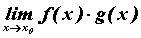 - неопределенность типа - неопределенность типа 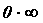 .
Рассматривают также неопределенности типа .
Рассматривают также неопределенности типа 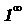 , , 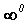 и т. д.
Основным признаком неопределенности является
невозможность корректного вычисления функции
простой подстановкой и т. д.
Основным признаком неопределенности является
невозможность корректного вычисления функции
простой подстановкой 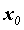 в выражение для
функции. Полезно запомнить замечательные
пределы: в выражение для
функции. Полезно запомнить замечательные
пределы:
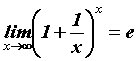 (е = 2.71828… - основание натуральных
логарифмов) - неопределенность типа (е = 2.71828… - основание натуральных
логарифмов) - неопределенность типа 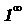 . .
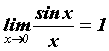 - неопределенность
типа - неопределенность
типа 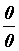 . .
ПРИМЕР 2 . Простейшие методы
раскрытия неопределенностей
Использование эквивалентных бесконечно
малых.
Если мы имеем неопределенность типа 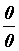 , то это
означает, что мы вычисляем предел отношения двух
бесконечно малых функций. Напомним, что функция
называется бесконечно малой, если ее предел в
точке , то это
означает, что мы вычисляем предел отношения двух
бесконечно малых функций. Напомним, что функция
называется бесконечно малой, если ее предел в
точке 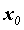 равен нулю. Пусть
равен нулю. Пусть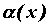 , , 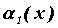 , , 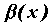 , , 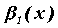 - бесконечно малые
функции при - бесконечно малые
функции при 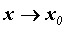 , причем , причем 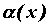 эквивалентна эквивалентна 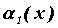 , т.е. , т.е.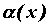 ~ ~ 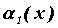 , , 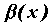 ~ ~ 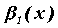 (напомним,
что две бесконечно малых называются
эквивалентными, если предел их отношения равен 1).
Тогда (напомним,
что две бесконечно малых называются
эквивалентными, если предел их отношения равен 1).
Тогда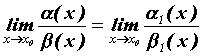 ,
т.е. при вычислении пределов отношений
бесконечно малых любую из них можно заменять на
эквивалентную. ,
т.е. при вычислении пределов отношений
бесконечно малых любую из них можно заменять на
эквивалентную.
ПРИМЕР 3 . Раскрытие
неопределенностей с помощью эквивалентных
бесконечно малых
Правило Лопиталя.
Неопределенности типа 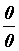 или или 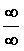 удобно раскрывать с
помощью правила Лопиталя. Пусть удобно раскрывать с
помощью правила Лопиталя. Пусть 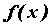 и и 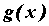 две бесконечно малые или бесконечно большие функции при две бесконечно малые или бесконечно большие функции при 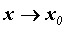 и
существует предел отношения их производных при и
существует предел отношения их производных при 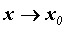 . Тогда . Тогда 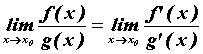 . Если в
результате применения правила Лопиталя снова
получится неопределенность, то его можно
применить еще раз. . Если в
результате применения правила Лопиталя снова
получится неопределенность, то его можно
применить еще раз.
ПРИМЕР 4. Раскрытие
неопределенностей с помощью правила Лопиталя
Формула Тейлора.
Пусть функция 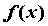 имеет в точке имеет в точке 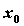 производные всех
порядков до производные всех
порядков до 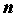 -го включительно. Тогда для -го включительно. Тогда для 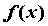 справедлива формула
Тейлора:
справедлива формула
Тейлора:
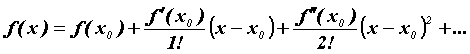
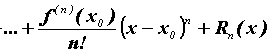
где 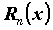 называется остаточным
членом формулы Тейлора.
называется остаточным
членом формулы Тейлора.
ПРИМЕР 5 . Раскрытие
неопределенностей с помощью формулы Тейлора

|

