Непрерывные
функции ~ Свойства функций,
непрерывных на отрезке
Непрерывные функции.
Рассмотрим функцию 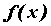 , определенную на
некотором промежутке , определенную на
некотором промежутке 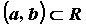 . Функция . Функция 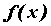 непрерывна
в точке непрерывна
в точке 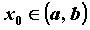 , если предел
функции в точке , если предел
функции в точке 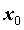 равен значению
функции в этой точке, равен значению
функции в этой точке,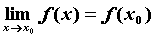 . .
ПРИМЕР 1 . Доказательство
непрерывности функции в точке.
Свойства функций, непрерывных на отрезке.
Функция, непрерывная в каждой точке промежутка 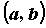 ,
называется непрерывной на промежутке. Для
функции, непрерывной на отрезке ,
называется непрерывной на промежутке. Для
функции, непрерывной на отрезке 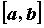 , справедливы
следующие утверждения. , справедливы
следующие утверждения.
Функция, непрерывная на отрезке 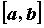 ,
достигает на нем своих наибольшего и наименьшего
значений, т.е. на отрезке ,
достигает на нем своих наибольшего и наименьшего
значений, т.е. на отрезке 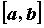 существуют точки существуют точки 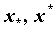 такие,
что такие,
что
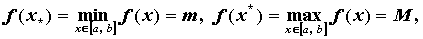
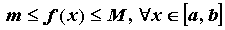 . .
Если функция 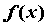 непрерывна на отрезке непрерывна на отрезке 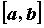 и принимает на концах
значения разных знаков, то на интервале и принимает на концах
значения разных знаков, то на интервале 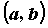 существует точка
существует точка 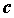 , в которой функция
обращается в нуль, т.е. , в которой функция
обращается в нуль, т.е. 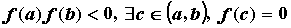 . Это утверждение
применяют для отделения корней уравнений . Это утверждение
применяют для отделения корней уравнений 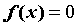 с
непрерывной левой частью — если найден отрезок,
на концах которого функция принимает значения
разных знаков, то можно утверждать, что на этом
отрезке есть хотя бы один корень уравнения. с
непрерывной левой частью — если найден отрезок,
на концах которого функция принимает значения
разных знаков, то можно утверждать, что на этом
отрезке есть хотя бы один корень уравнения.
Если функция 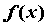 непрерывна на отрезке непрерывна на отрезке
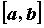 , дифференцируема хотя
бы на интервале , дифференцируема хотя
бы на интервале 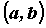 , то на интервале , то на интервале 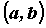 существует точка существует точка 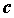 , такая,
что , такая,
что 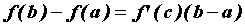 . Это свойство называют формулой
Лагранжа или формулой конечных приращений. . Это свойство называют формулой
Лагранжа или формулой конечных приращений.
ПРИМЕР 2 . Нахождение
наибольшего и наименьшего значения непрерывной
функции на отрезке.
ПРИМЕР 3 . Отделение корней
уравнения f(x)=0 с непрерывной левой частью.
ПРИМЕР 4. Геометрический
смысл формулы Лагранжа.

|

