Интеграл
как функция верхнего предела ~Несобственные
интегралы по неограниченному промежутку ~ Несобственные интегралы от
неограниченных функций ~ Исследование
несобственных интегралов на сходимость
Интеграл как функция верхнего предела.
Для функции 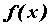 , интегрируемой для всех , интегрируемой для всех 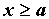 ,
значение интеграла ,
значение интеграла 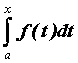 зависит от значения
верхнего предела зависит от значения
верхнего предела 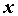 ; можно рассмотреть
функцию переменной ; можно рассмотреть
функцию переменной 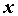 : каждому значению : каждому значению 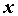 ставится в соответствие число, равное значению
интеграла
ставится в соответствие число, равное значению
интеграла 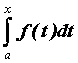 . Таким образом, можно рассматривать
определенный интеграл как функцию верхнего
предела: . Таким образом, можно рассматривать
определенный интеграл как функцию верхнего
предела: 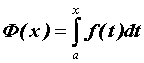 ; функция ; функция 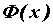 определена в области
интегрируемости подынтегральной функции определена в области
интегрируемости подынтегральной функции 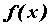 . Если . Если 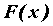 — первообразная для — первообразная для 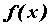 , то
значение , то
значение 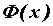 можно вычислить по формуле Ньютона—Лейбница: можно вычислить по формуле Ньютона—Лейбница: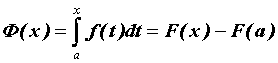 .
Функцию .
Функцию 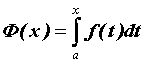 можно исследовать, не вычисляя
первообразной. Для интегрируемой при можно исследовать, не вычисляя
первообразной. Для интегрируемой при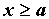 функции
функции 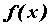 справедливы следующие утверждения: справедливы следующие утверждения: 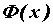 непрерывна на
промежутке непрерывна на
промежутке 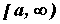 , причем , причем 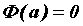 ; если ; если 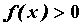 при при 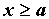 , то , то
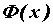 монотонно возрастает на промежутке монотонно возрастает на промежутке 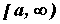 ; если ; если 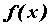 непрерывна
при непрерывна
при 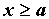 ,
то ,
то 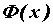 дифференцируема на
промежутке дифференцируема на
промежутке 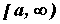 , причем , причем 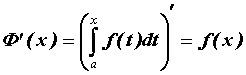 . .
ПРИМЕР 1 . Исследование
функции, заданной интегралом.
Несобственные интегралы по
неограниченному промежутку.
Пусть функция 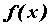 интегрируема для
всех интегрируема для
всех 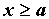 и
и 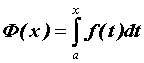 . Если существует предел . Если существует предел 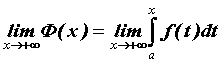 , то этот предел
называют несобственным интегралом по
неограниченному промежутку и обозначают его , то этот предел
называют несобственным интегралом по
неограниченному промежутку и обозначают его 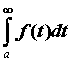 . Если
предел конечен, то говорят, что несобственный
интеграл сходится и его значение вычисляют по
формуле . Если
предел конечен, то говорят, что несобственный
интеграл сходится и его значение вычисляют по
формуле 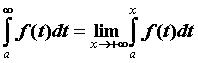 . Аналогично определен интеграл . Аналогично определен интеграл 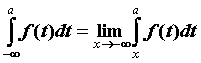 для
интегрируемой при для
интегрируемой при 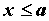 функции функции 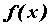 и
интеграл и
интеграл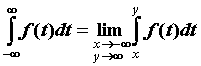 для функции , интегрируемой на для функции , интегрируемой на 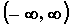 . Если
рассмотренные пределы бесконечны, то говорят,
что соответствующий несобственный интеграл
расходится. . Если
рассмотренные пределы бесконечны, то говорят,
что соответствующий несобственный интеграл
расходится.
ПРИМЕР 2 . Вычисление
несобственного интеграла с бесконечным пределом.
Несобственные интегралы от
неограниченных функций.
Пусть функция 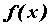 интегрируема на
любом отрезке, целиком содержащемся в промежутке интегрируема на
любом отрезке, целиком содержащемся в промежутке
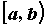 , и бесконечно большая в
точке , и бесконечно большая в
точке 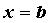 . Если существует предел . Если существует предел 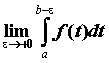 , то
этот предел называют несобственным интегралом
от неограниченной функции , то
этот предел называют несобственным интегралом
от неограниченной функции 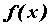 по по 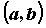 и обозначают его и обозначают его 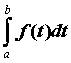 . Если
предел конечен, то говорят, что несобственный
интеграл сходится и его значение вычисляют по
формуле . Если
предел конечен, то говорят, что несобственный
интеграл сходится и его значение вычисляют по
формуле 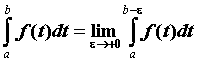 . Аналогично определен интеграл . Аналогично определен интеграл 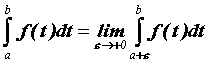 от
интегрируемой на любом конечном отрезке,
содержащемся в от
интегрируемой на любом конечном отрезке,
содержащемся в 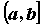 , бесконечно большой в
точке , бесконечно большой в
точке 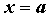 функции функции 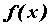 . Если пределы
бесконечны, то говорят, что соответствующий
несобственный интеграл расходится. . Если пределы
бесконечны, то говорят, что соответствующий
несобственный интеграл расходится.
ПРИМЕР 3 . Вычисление
несобственного интеграла от неограниченной
функции.
Исследование несобственных интегралов
на сходимость.
Вычисление несобственных интегралов сводится
к вычислению первообразной,
использованию формулы
Ньютона-Лейбница и вычислению предела. Каждый из этапов сам по себе
достаточно сложен, и разумно приступать к ним,
если есть уверенность, что интеграл сходится, то
есть предел конечен. Поэтому, в конечном счете,
самым важным в теории несобственных интегралов
является исследование их на сходимость: если
интеграл расходится, то его и вычислять не надо.
Одним из главных инструментов исследования
несобственных интегралов на сходимость являются
теоремы сравнения.
Рассмотрим две неотрицательные функции 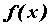 и и 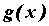 ,
определенные при ,
определенные при 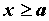 . Пусть . Пусть 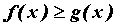 для
всех для
всех 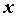 , начиная с некоторого числа
, начиная с некоторого числа 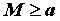 . Тогда, если сходится
интеграл от большей функции . Тогда, если сходится
интеграл от большей функции 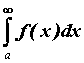 , то сходится и
интеграл от меньшей, то есть , то сходится и
интеграл от меньшей, то есть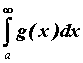 . Если расходится
интеграл от меньшей функции . Если расходится
интеграл от меньшей функции 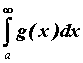 ,то расходится и
интеграл от большей - ,то расходится и
интеграл от большей - 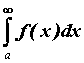 . .
Если 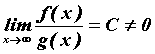 , то несобственные интегралы от этих
функций или оба сходятся или оба расходятся. , то несобственные интегралы от этих
функций или оба сходятся или оба расходятся.
Аналогичные утверждения, которые называют
признаками сравнения, имеют место и для
интегралов по конечному промежутку от
неограниченных функций.
ПРИМЕР 4. Исследование
несобственных интегралов на сходимость.

|

