Определенный
интеграл, его геометрический смысл ~Формула Ньютона-Лейбница ~ Методы вычисления определенного
интеграла
Определенный интеграл, его
геометрический смысл.
Рассмотрим функцию 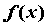 , определенную на
промежутке , определенную на
промежутке 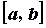 . Разобьем промежуток на . Разобьем промежуток на 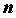 произвольных частей точками
произвольных частей точками 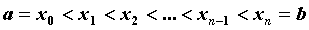 и обозначим и обозначим 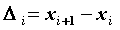 , , 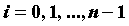 , , 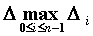 . На
каждом промежутке . На
каждом промежутке 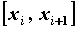 возьмем произвольную
точку возьмем произвольную
точку 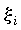 и вычислим в ней значение функции
и вычислим в ней значение функции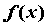 .
Выражение .
Выражение 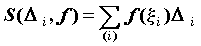 называется интегральной суммой
функции называется интегральной суммой
функции 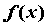 на на 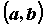 .Если при .Если при 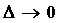 существует и конечен предел
последовательности частичных сумм
существует и конечен предел
последовательности частичных сумм 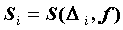 , не
зависящий ни от способа разбиения промежутка , не
зависящий ни от способа разбиения промежутка 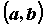 точками
точками 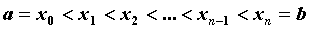 , ни от выбора , ни от выбора 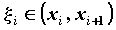 , то этот предел
называют определенным интегралом от функции , то этот предел
называют определенным интегралом от функции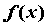 по
промежутку по
промежутку 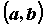 , а саму функцию — интегрируемой на , а саму функцию — интегрируемой на 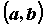 .
Обозначают .
Обозначают 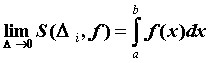 . .
Из приведенного определения естественно
следует геометрический смысл определенного
интеграла: если 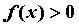 , то , то 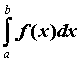 равен
площади фигуры, ограниченной графиком функции,
осью абсцисс и прямыми равен
площади фигуры, ограниченной графиком функции,
осью абсцисс и прямыми 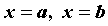 . .
ПРИМЕР 1 . Вычисление
определенного интеграла как предела
интегральной суммы.
Формула Ньютона-Лейбница.
Значение определенного интеграла может быть
вычислено по формуле Ньютона-Лейбница 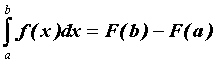 = =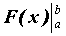 , здесь
символ , здесь
символ 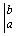 означает, что из значения означает, что из значения 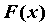 при
верхнем пределе b нужно вычесть значение при
нижнем пределе a , при
верхнем пределе b нужно вычесть значение при
нижнем пределе a , 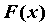 — первообразная функция для — первообразная функция для 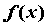 . Таким
образом, вычисление определенного интеграла
сводится к нахождению первообразной, то есть неопределенного
интеграла. . Таким
образом, вычисление определенного интеграла
сводится к нахождению первообразной, то есть неопределенного
интеграла.
ПРИМЕР 2 . Вычисление
определенного интеграла.
Методы вычисления определенного
интеграла.
Если 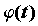 — непрерывно дифференцируемая
на отрезке — непрерывно дифференцируемая
на отрезке 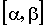 функция, функция, 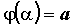 , , 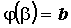 и и 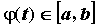 , когда , когда 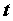 изменяется на
изменяется на 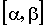 , то, положив , то, положив 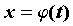 , получим формулу
замены переменной в определенном интеграле , получим формулу
замены переменной в определенном интеграле 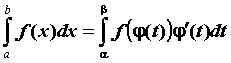 . .
Пусть 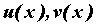 - непрерывно дифференцируемые функции.
Тогда справедлива формула интегрирования по
частям - непрерывно дифференцируемые функции.
Тогда справедлива формула интегрирования по
частям 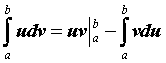 . Эта формула применяется для тех же
классов функций, что и при вычислении
неопределенного интеграла. . Эта формула применяется для тех же
классов функций, что и при вычислении
неопределенного интеграла.
ПРИМЕР 3 . Замена переменной
и интегрирование по частям в определенном
интеграле

|

