Первообразная
и неопределенный интеграл ~ Интегрирование
заменой переменной ~ Интегрирование
по частям
Первообразная и неопределенный интеграл
- Рассмотрим функцию 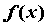 ,
определенную на промежутке ,
определенную на промежутке 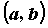 (здесь
возможно (здесь
возможно 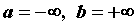 ). Дифференцируемая
на промежутке ). Дифференцируемая
на промежутке 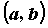 функция функция 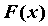 , производная которой в каждой точке равна , производная которой в каждой точке равна 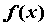 , называется первообразной функции , называется первообразной функции 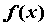 : : 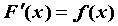 . Поскольку . Поскольку 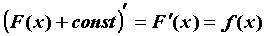 , то можно говорить о семействе
первообразных — множестве функций вида , то можно говорить о семействе
первообразных — множестве функций вида 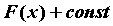 , , 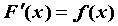 . Семейство
первообразных . Семейство
первообразных 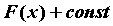 функции функции 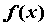 называется неопределенным интегралом
функции называется неопределенным интегралом
функции 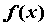 и обозначается символом и обозначается символом 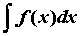 : :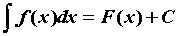 для всех для всех 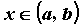 .
Здесь .
Здесь 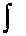 — знак интеграла, — знак интеграла, 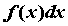 — подынтегральное выражение, — подынтегральное выражение, 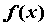 — подынтегральная функция, — подынтегральная функция, 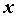 — переменная интегрирования, — переменная интегрирования, 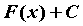 — значение неопределенного интеграла,
семейство первообразных функции — значение неопределенного интеграла,
семейство первообразных функции 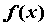 , , 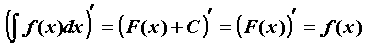 . То есть производная неопределенного интеграла
равна подынтегральной функции. Наоборот, . То есть производная неопределенного интеграла
равна подынтегральной функции. Наоборот, 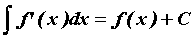 , следовательно, дифференцирование и
вычисление неопределенного интеграла, – взаимно
обратные операции. Не представляет труда с
помощью таблицы производных составить таблицу
неопределенных интегралов. Важным свойством
неопределенного интеграла является линейность: , следовательно, дифференцирование и
вычисление неопределенного интеграла, – взаимно
обратные операции. Не представляет труда с
помощью таблицы производных составить таблицу
неопределенных интегралов. Важным свойством
неопределенного интеграла является линейность: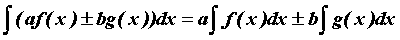 , здесь , здесь 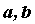 -
постоянные. Вычисление неопределенного
интеграла обычно сводится к преобразованию
подынтегрального выражения так, чтобы можно было
воспользоваться таблицей интегралов. -
постоянные. Вычисление неопределенного
интеграла обычно сводится к преобразованию
подынтегрального выражения так, чтобы можно было
воспользоваться таблицей интегралов.
ПРИМЕР 1. Простейшие методы
интегрирования
Интегрирование заменой переменной -
Если 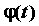 — непрерывно дифференцируемая
функция, то, полагая — непрерывно дифференцируемая
функция, то, полагая 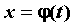 , получим
формулу интегрирования заменой
переменной , получим
формулу интегрирования заменой
переменной 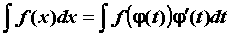 . Если
замена переменной выбрана правильно, то интеграл
в правой части должен легко вычисляться. Для
некоторых классов функций существуют
стандартные замены, сводящие интеграл к
табличному. . Если
замена переменной выбрана правильно, то интеграл
в правой части должен легко вычисляться. Для
некоторых классов функций существуют
стандартные замены, сводящие интеграл к
табличному.
ПРИМЕР 2. Замена переменной
в неопределенном интеграле
Интегрирование по частям - Пусть 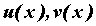 - непрерывно дифференцируемые
функции. Тогда справедлива формула
интегрирования по частям - непрерывно дифференцируемые
функции. Тогда справедлива формула
интегрирования по частям 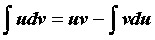 .
Название “по частям” связано с тем, что для
записи интеграла в правой части нужно
проинтегрировать “часть” .
Название “по частям” связано с тем, что для
записи интеграла в правой части нужно
проинтегрировать “часть” 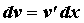 подынтегрального выражения в левой части.
Метод интегрирования по частям используется для
интегралов вида подынтегрального выражения в левой части.
Метод интегрирования по частям используется для
интегралов вида 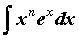 , , 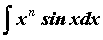 , , 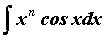 , , 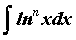 и
некоторых других. и
некоторых других.
ПРИМЕР 3. Интегрирование по
частям в неопределенном интеграле

|

