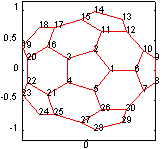
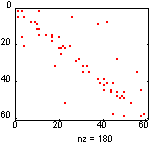
Синтаксис:

            r = symrcm(S)

Описание:

Функция r = symrcm(S) возвращает такой вектор упорядоченности для симметрической матрицы S, что S(r, r) будет концентрировать ненулевые элементы вблизи диагонали. Это хорошее упорядочение как для LU-, так и для LL^T-разложения матрицы, что позволяет отказаться от работы с элементами, удаленными от диагонали. Такое упорядочение называется упорядочением Катхилла - Макки (Cuthill - McKee).

Для действительных симметрических разреженных матриц собственные значения S(r, r) совпадают с собственными значениями S, но времени на вычисление eig(S(r, r)) будет затрачиваться существенно меньше, чем для eig(S).

Пример:

Рассмотрим матрицу bucky размера 60 х 60, которую связывают с футбольным мячом, куполом (Buckminster Fuller dome, отсюда название bucky), а в последнее время - с моделью атома углерода C₆₀. Ее граф имеет 60 вершин, которые пронумерованы так, что половина из них находится в одной, а половина в другой полусфере (рис. а), и эти половины соединены вместе. Такая нумерация приводит к структуре матрицы, изображенной на рис. б.

а)	б)

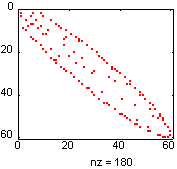
Применяя RCM-упорядочение

               p = symrcm(B);
               R = B(p, p);
               spy(R)

получим матрицу с узкой полосой вблизи диагонали (рис. в), ширина которой может быть вычислена следующим образом:

               [i, j] = find(B);
               bw = max(i - j) + 1

Ширина полосы матрицы A равна 35, а матрицы R - 12.

в)

Сопутствующие функции: COLMMD, COLPERM, LU, CHOL, EIG, \.

Ссылки:

1. George A., Liu J. Сomputer Solution of Large Sparse Positive Definite Systems. Prentice-Hall, 1981.

2. Gilbert J. R., Moler C., Schreiber R. Sparse Matrices in MATLAB: Design and Implementation//SIAM Journal on Matrix Analysis and Applications. 1992. Vol. 13. P. 333-356.