Математическое
ожидание ~ Дисперсия ~ Условное
математическое ожидание ~ Ковариация
~ Корреляция
В этом разделе рассмотрены числовые
характеристики только двумерных случайных
величин, поскольку обобщение на случай 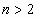 не вызывает
затруднений. не вызывает
затруднений.
Математическое ожидание
Пусть (x , h ) -
двумерная случайная величина, тогда M(x , h )=(M(x ), M(h )),
т.е. математическое ожидание случайного вектора -
это вектор из математических ожиданий компонент
вектора.
Если (x , h ) -
дискретный случайный вектор с распределением
| |
y1 |
y2 |
... |
ym |
| x1 |
p11 |
p12 |
... |
p1m |
| x2 |
p12 |
p12 |
... |
p2m |
| ... |
... |
... |
pij |
... |
| xn |
pn1 |
pn2 |
... |
pnm |
то математические ожидания компонент
вычисляются по формулам:
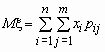 , , 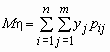 . .
Эти формулы можно записать в сокращенном виде.
Обозначим 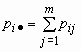 и и 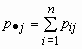 , тогда , тогда 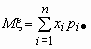 и и 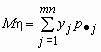 . .
Если p(x , h )(x,
y)- совместная плотность распределения
непрерывной двумерной случайной величины (x , h ), то
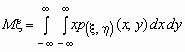 и и 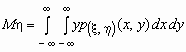 . .
Поскольку 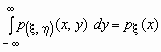 -плотность распределения случайной величины x , то
-плотность распределения случайной величины x , то 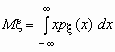 и, аналогично, и, аналогично, 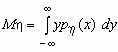 . .
Дисперсия
Понятие дисперсии обобщается на многомерные
случайные величины нетривиальным образом. Это
обобщение будет сделано в следующем разделе.
Здесь лишь приведем формулы для вычисления
дисперсии компонент двумерного случайного
вектора.
Если (x , h ) -
двумерная случайная величина, то
Dx = M(x - Mx )2 =
Mx 2 - M(x )2, Dh =
M(h - Mh
)2 = Mh 2 - M(h )2.
Входящие в эту формулу математические ожидания
вычисляются по приведенным выше формулам.
Условное математическое ожидание
Между случайными величинами может
существовать функциональная зависимость.
Например, если x - случайная
величина и h =x 2,
то h - тоже случайная величина,
связанная с x функциональной
зависимостью. В то же время между случайными
величинами может существовать зависимость
другого рода, называемая стохастической. В
разделе, посвященном условным распределениям
уже обсуждалась такая зависимость. Из
рассмотренных там примеров видно, что информация
о значении одной случайной величины (одной
компоненты случайного вектора) изменяет
распределение другой случайной величины (другой
компоненты случайного вектора), а это может,
вообще говоря, изменить и числовые
характеристики случайных величин.
Математическое ожидание, вычисленное по
условному распределению, называется условным
математическим ожиданием.
Для двумерного дискретного случайного
вектора (x , h ) с
распределением
| |
y1 |
y2 |
... |
ym |
| x1 |
p11 |
p12 |
... |
p1m |
| x2 |
p12 |
p12 |
... |
p2m |
| ... |
... |
... |
pij |
... |
| xn |
pn1 |
pn2 |
... |
pnm |
условное математическое ожидание случайной
величины x при условии, что
случайная величина h принимает
значение yj, вычисляется по формуле 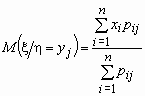 . .
Аналогично, условное математическое ожидание
случайной величины h при условии,
что случайная величина x принимает
значение xi, равно 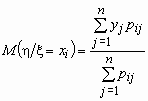 . .
Видно, что условное математическое ожидание
случайной величины x является
функцией значений случайной величины h
, т.е. M(x /h
= y) = f1(y) и, совершенно
аналогично, M(h /x = x) = f2(x).
Функцию f1(y) называют регрессией
случайной величины x на случайную
величину h , а f2(x) - регрессией
случайной величины h на случайную
величину x .
Если p(x ,h )(x,
y) совместная плотность вероятностей
двумерной случайной величины (x ,h ), то
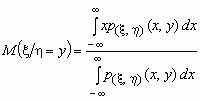 и и 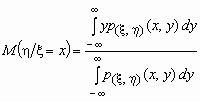 . .
Ковариация
Если между случайными величинами x
и h существует стохастическая
связь, то одним из параметров, характеризующих
меру этой связи является ковариация cov(x , h ). Ковариацию
вычисляют по формулам cov(x , h )=M[(x - Mx )(h - Mh )] = M(x h) - Mx Mh .
Если случайные величины x и h независимы, то cov(x
,h )=0.
Обратное, вообще говоря, неверно. Из равенства
нулю ковариации не следует независимость
случайных величин. Случайные величины могут быть
зависимыми в то время как их ковариация нулевая!
Но зато, если ковариация случайных величин
отлична от нуля, то между ними существует
стохастическая связь, мерой которой и является
величина ковариации.
Свойства ковариации:
cov(x , x ) = Dx ;
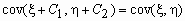 ; ;
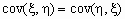 ; ;
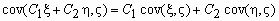 , ,
где C1 и C2 - произвольные
константы.
Ковариационной матрицей случайного вектора (x ,h ) называется
матрица вида
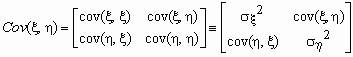 . .
Эта матрица симметрична и положительно
определена. Ее определитель называется обобщенной
дисперсией и может служить мерой рассеяния
системы случайных величин (x ,h ).
Как уже отмечалось ранее, дисперсия суммы независимых
случайных величин равна сумме их дисперсий: 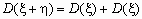 . Если же
случайные величины зависимы, то . Если же
случайные величины зависимы, то 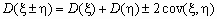 . .
Корреляция
Понятно, что значение ковариации зависит не
только от “тесноты” связи случайных величин, но
и от самих значений этих величин, например, от
единиц измерения этих значений. Для исключения
этой зависимости вместо ковариации используется
безразмерный коэффициент корреляции 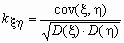 . .
Этот коэффициент обладает следующими
свойствами:
он безразмерен;
его модуль не превосходит единицы, т.е. 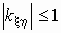 ; ;
если x и h
независимы, то k(x ,h
)=0 (обратное неверно!);
если 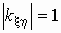 , то
случайные величины x и h
связаны функциональной зависимостью вида , то
случайные величины x и h
связаны функциональной зависимостью вида
h = ax +b,
где a и b- некоторые числовые
коэффициенты;
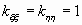 ; ;
Корреляционной матрицей случайного вектора называется
матрица
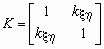 . .
Если 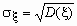 и и 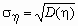 , то ковариационная и
корреляционная матрицы случайного вектора (x ,h ) связаны
соотношением , то ковариационная и
корреляционная матрицы случайного вектора (x ,h ) связаны
соотношением 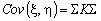 , где , где
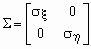 . .

|

