Многомерные
случайные величины. Функции распределения
многомерных случайных величин ~ Независимость
случайных величин ~ Условные
распределения случайных величин ~ Условные
распределения дискретных случайных величин ~ Условные распределения непрерывных
случайных величин
В одном и том же случайном эксперименте можно
рассматривать не одну, а несколько - n -
числовых функций, определенных на одном и том же
пространстве элементарных событий. Совокупность
таких функций называется многомерной
случайной величиной или случайным вектором
и обозначается 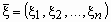 . .
Точнее. На вероятностном пространстве 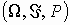 заданы случайные
величины заданы случайные
величины 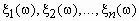 ;
каждому w ;
каждому w  W
эти величины ставят в соответствие n-мерный
вектор W
эти величины ставят в соответствие n-мерный
вектор 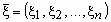 ,
который называется n-мерным случайным
вектором (n-мерной случайной величиной). ,
который называется n-мерным случайным
вектором (n-мерной случайной величиной).
Многомерные случайные величины.
Функции распределения многомерных случайных
величин.
Функцией распределения случайного вектора 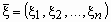 или совместным
распределением случайных величин или совместным
распределением случайных величин 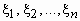 называется функция,
определенная равенством называется функция,
определенная равенством
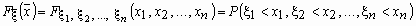 , ,
где 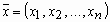 . .
По известной многомерной функции 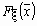 можно найти
распределение каждой из компонент можно найти
распределение каждой из компонент 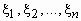 . .
Например, если 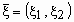 -
двумерная случайная величина, имеющая
совместное распределение -
двумерная случайная величина, имеющая
совместное распределение 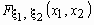 , то распределения компонент , то распределения компонент 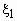 и и 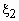 вычисляются
соответственно по формулам: вычисляются
соответственно по формулам:
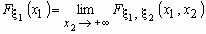 , , 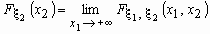 . .
В дальнейшем будем рассматривать двумерные
случайные векторы.
Случайный вектор 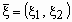 называется непрерывным случайным вектором,
если существует такая неотрицательная функция
называется непрерывным случайным вектором,
если существует такая неотрицательная функция 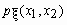 , что для
любого прямоугольника W на
плоскости , что для
любого прямоугольника W на
плоскости 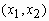 вероятность события
вероятность события 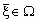 равна
равна
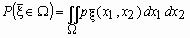 . .
Функция 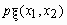 в этом случае называется совместной плотностью
распределения.
в этом случае называется совместной плотностью
распределения.
Легко показать, что 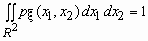 . .
Если 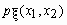 -
совместная плотность распределения двумерного
случайного вектора -
совместная плотность распределения двумерного
случайного вектора 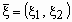 ,
то плотности распределения его компонент
определяются равенствами: ,
то плотности распределения его компонент
определяются равенствами:
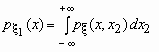 и и 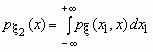 . .
Если 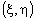 - дискретный
случайный вектор, то совместным распределением
случайных величин - дискретный
случайный вектор, то совместным распределением
случайных величин 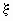 и и 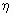 чаще всего называют
таблицу вида чаще всего называют
таблицу вида
| |
y1 |
y2 |
... |
ym |
| x1 |
p11 |
p12 |
... |
p1m |
| x2 |
p21 |
p22 |
... |
p2m |
| ... |
... |
... |
pij |
... |
| xn |
pn1 |
pn2 |
... |
pnm |
где 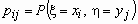 и и 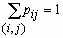 . .
По этой таблице можно найти распределения 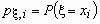 и и 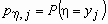 компонент x и h
. Они вычисляются по формулам: компонент x и h
. Они вычисляются по формулам:
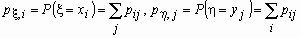 . .
Независимость случайных величин
Решить обратную задачу, т.е. восстановить
совместное распределение (x , h ) по распределениям величин x и h , вообще говоря,
невозможно. Однако эту задачу можно решить, когда
случайные величины x и h
независимы.
Случайные величины x и h
называются независимыми, если для любых x1,
x2  R2
справедливо равенство: R2
справедливо равенство:
Fx ,h (x1,
x2)= Fx (x1)Fh ( x2).
Для непрерывных случайных величин это
определение эквивалентно следующему:
случайные величины называются независимыми,
если
px ,h (x1,
x2)= px (x1)
ph (x2)
во всех точках непрерывности входящих в это
равенство функций.
Для дискретных случайных величин x
и h с матрицей совместного
распределения {pij} условие
независимости x и h
имеет вид:
pij = P(x = xi, h = yj) = P(x =
xi) P(h = yj),
для всех i = 1, 2, …, n, j = 1, 2, …, m.
Условные распределения случайных
величин
Если две случайные величины x и h зависимы, то информация о том,
какое значение на самом деле приняла одна из них,
меняет наше представление о распределении
другой. В связи с этим можно ввести понятие условного
распределения.
Условные распределения дискретных
случайных величин
Пусть дана двумерная случайная величина (x ,h ) с
распределением
| |
y1 |
y2 |
... |
ym |
| x1 |
p11 |
p12 |
... |
p1m |
| x2 |
p12 |
p12 |
... |
p2m |
| ... |
... |
... |
pij |
... |
| xn |
pn1 |
pn2 |
... |
pnm |
Тогда распределения случайных величин x и h имеют
соответственно вид:
| x |
x1 |
x2 |
... |
xn |
| p |
p1·
|
p2·
|
... |
pn·
|
| h |
y1 |
y2 |
... |
yn |
 |
p· 1 |
p· 2 |
... |
p· n |
точка · в индексе означает
суммирование по строкам или по столбцам:
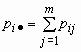 , , 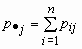 . .
Условным распределением случайной
величины 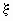 при условии, что случайная величина
при условии, что случайная величина 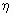 приняла значение приняла значение 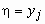 , называется
распределение: , называется
распределение:
Нетрудно убедиться, что сумма вероятностей
величины 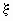 в этом распределении равна единице:
в этом распределении равна единице: 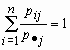 для всех j = 1, 2, …, m. для всех j = 1, 2, …, m.
Совершенно аналогично условным
распределением случайной величины 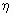 при условии, что
случайная величина при условии, что
случайная величина 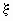 приняла значение приняла значение 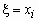 , называется распределение: , называется распределение:
И 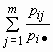 для всех i = 1, 2,
…, n. для всех i = 1, 2,
…, n.
Если условные распределения случайных величин x и h отличаются от их
безусловных распределений, то случайные
величины x и h зависимы.
Условные распределения непрерывных
случайных величин
Если 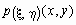 - плотность
вероятностей совместного распределения
двумерной случайной величины - плотность
вероятностей совместного распределения
двумерной случайной величины 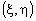 , то плотности вероятностей каждой ее
компоненты вычисляются по формулам: , то плотности вероятностей каждой ее
компоненты вычисляются по формулам:
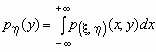 , , 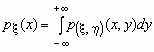 . .
Условной плотностью распределения случайной
величины x при условии, что
случайная величина h принимает
значение h = y0, называется
функция переменной x, определяемая формулой
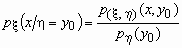 . .
Аналогично, условной плотностью
распределения случайной величины 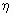 при условии, что
случайная величина x принимает
значение x = x0, называется
функция переменной y, определяемая формулой при условии, что
случайная величина x принимает
значение x = x0, называется
функция переменной y, определяемая формулой
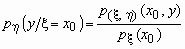 . .

|

