Плотность
вероятности суммы двух случайных величин ~ Распределение произведения двух
случайных величин
Если x - случайная величина с
областью значений Xx и
функция f(x) определена на множестве Xx , то h = f(x)
- тоже случайная величина. Задача об отыскании
функции распределения случайной величины h по известной функции распределения
случайной величины x легко
решается, если f(x) - непрерывная монотонно
возрастающая функция. Доказано, что тогда
функция распределения Fh (x)
случайной величины h задается
формулой Fh (x)=Fx ([f(x)]-1).
Здесь Fx (x) -
известная функция распределения случайной
величины x , а символом [f(x)]-1
обозначена функция, обратная к функции f(x).
Плотность распределения случайной величины h для дифференцируемой f(x)
вычисляется по формуле
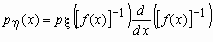 . .
Плотность вероятности суммы двух
случайных величин
В теории вероятностей часто возникает
необходимость в определении плотности
вероятности суммы двух независимых случайных
величин. Если x 1 и x
2 - непрерывные независимые случайные
величины с плотностями вероятности
соответственно p1(x) и p2(x),
то плотность вероятностей суммы h =
x 1 + x 2
вычисляется по формуле:
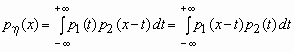 . .
Распределение произведения двух
случайных величин
Порядок построения распределения произведения
двух дискретных случайных величин проще всего
объяснить на примере.
Пусть (x , h ) -
дискретный случайный вектор с распределением:
| |
1 |
2 |
3 |
4 |
| 0 |
0.01 |
0.02 |
0.03 |
0.04 |
| 1 |
0.1 |
0.1 |
0.2 |
0.4 |
| 2 |
0.05 |
0.01 |
0.01 |
0.03 |
Найдем распределение произведения случайных
величин - случайной величины z = x * h,
которая принимает значения 0, 1, 2, 3, 4, 6, 8.
Вычислим соответствующие вероятности:
P(z = x * h = 0) = P(x
= 0, h = 1) + P(x = 0, h = 2) + P(x = 0, h = 3) + P(x = 0, h = 4) = 0.1;
P(z = 1) = P(x = 1,
h = 1) =0.1; P(z = 2) = P(x = 1, h = 2) + P(x = 2, h = 1) =0.15; и т.д.
В результате получим распределение случайной
величины z = x * h :
 z z |
0 |
1 |
2 |
3 |
4 |
6 |
8 |
| p |
0.1 |
0.1 |
0.15 |
0.2 |
0.41 |
0.01 |
0.03 |
Для того чтобы найти распределение
произведения непрерывных случайных величин,
необходимо выполнить более громоздкие
вычисления.
Пусть (x , h ) -
непрерывный двумерный случайный вектор с
плотностью распределения p(x
h )(x1, x2).
Построим функцию распределения случайной
величины z =x * h . Согласно
определению
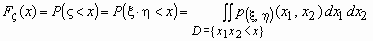 . .
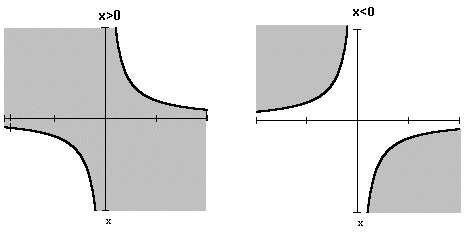
Для вычисления этой вероятности рассмотрим
отдельно случаи x>0 и x<0. Области
интегрирования для обоих случаев на рисунке
закрашены.
Область D={ x1x2 < x, x > 0}
изображена на рисунке слева, а область D={ x1x2
< x, x < 0} - справа.
При x>0 имеем: 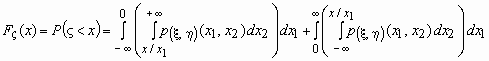 . .
При x<0: 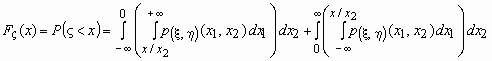 . .

|

