Теорема Пуассона ~
Локальная теорема Муавра—Лапласа ~ Интегральная теорема Муавра—Лапласа ~
Теорема Бернулли
Если число испытаний n в схеме независимых
испытаний Бернулли растет, а вероятность p
уменьшается, то точная формула 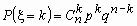 практически
непригодна из-за громоздких вычислений и
возникающих погрешностей округления. В этом
случае пользуются приближенными формулами
Пуассона (при npq < 9) и Муавра-Лапласа (npq >
9). практически
непригодна из-за громоздких вычислений и
возникающих погрешностей округления. В этом
случае пользуются приближенными формулами
Пуассона (при npq < 9) и Муавра-Лапласа (npq >
9).
Теорема Пуассона
Если число испытаний n в схеме независимых
испытаний Бернулли стремится к бесконечности и 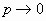 так, что так, что 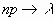 , , 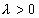 , то при любых , то при любых 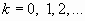
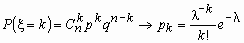
Это означает, что при больших n и малых p
вместо громоздких вычислений по точной формуле 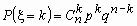 можно
воспользоваться приближенной формулой можно
воспользоваться приближенной формулой
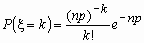 , т.е.
использовать формулу Пуассона для l
= np. , т.е.
использовать формулу Пуассона для l
= np.
На практике пуассоновским приближением
пользуются при npq < 9.
Локальная теорема Муавра-Лапласа
Пусть 0< p <1 и величина 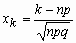 при n ® при n ®  ограничена.
Тогда ограничена.
Тогда 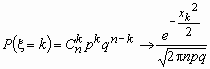 . .
На практике приближением Муавра-Лапласа
пользуются при npq > 9.
Точность формулы 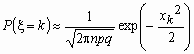 растет,
как с ростом величин n и k, так и по мере
приближения величин p и q к 0.5. растет,
как с ростом величин n и k, так и по мере
приближения величин p и q к 0.5.
Интегральная теорема Муавра-Лапласа
Пусть 0< p <1, тогда для схемы Бернулли при n
® 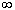 для любых a и b справедлива
формула для любых a и b справедлива
формула
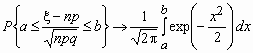 . .
Отсюда, в частности, следует, что для вычисления
вероятности того, что число успехов в n
испытаниях Бернулли заключено между k1 и
k2, можно использовать формулу
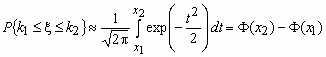 , ,
где 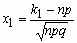 , , 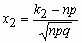 , , 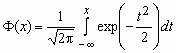 - функция Лапласа. - функция Лапласа.
Точность этой приближенной формулы растет с
ростом n.
Если npq сравнительно невелико, то лучшее
приближение дает формула
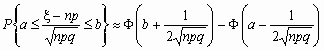
и для вычисления вероятности того, что число
успехов в n испытаниях Бернулли заключено
между k1 и k2, можно
использовать формулу
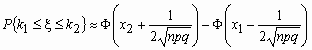 , где , где 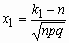 , , 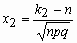 . .
Теорема Бернулли
Если x - число успехов в n испытаниях
Бернулли с вероятностью успеха в одном испытании
p, 0 < p < 1, то для любого e
> 0 справедливо: 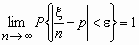 . .
Утверждение теоремы Бернулли означает, что с
ростом числа испытаний n относительная
частота успехов x /n
приближается к вероятности p успеха в одном
испытании.
Достаточно часто возникает необходимость
установить, сколько нужно произвести испытаний,
чтобы отклонение относительной частоты успехов x /n от вероятности p с
вероятностью, больше или равной 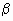 было меньше было меньше 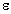 . Т.е. требуется найти n, для
которого справедливо неравенство . Т.е. требуется найти n, для
которого справедливо неравенство 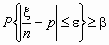 . Доказано, что число n,
которое обеспечивает выполнение этого
неравенства, удовлетворяет соотношению . Доказано, что число n,
которое обеспечивает выполнение этого
неравенства, удовлетворяет соотношению 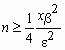 , где , где 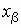 - решение уравнения - решение уравнения 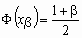 . Следует обратить особое внимание на
замечательный факт: искомое значение n не
зависит от p! . Следует обратить особое внимание на
замечательный факт: искомое значение n не
зависит от p!

|

